堆是实现优先级队列 效率很高的数据结构,如C++STL priority_queue、Python PriorityQueue。堆的变体很多,二叉堆、斐波那契堆…由堆实现的一种高效排序算法为堆排序。
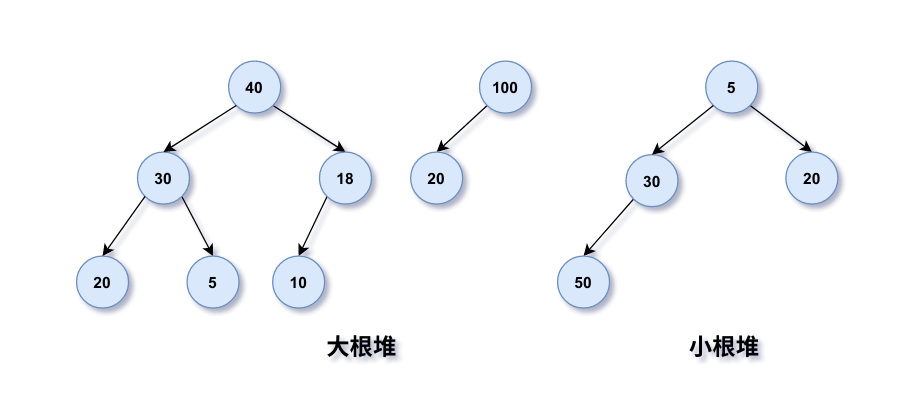
注意:数据结构中的堆和内存中的堆是两个完全不同的概念,就像数据结构栈和栈内存一样,之间没有必然联系。堆(Heap)也可称为大/小根堆、大/小根树,最大/小堆:
其中每个节点的值大于等于或小于等于其子节点(如果存在)的值;
一个大根堆(小根堆)是完全二叉树。
二叉堆由J.W.J.Williams于1964年引入,作为堆排序的数据结构。堆指的是二叉堆(Binary heap) 。数组描述,也可以用链表描述,不过数组描述比较普遍。
二叉堆中某个节点的左右子节点无论谁大谁小,只要满足子节点的值小于其父节点的值(最大堆)或大于其父节点的值(最小堆)即可。
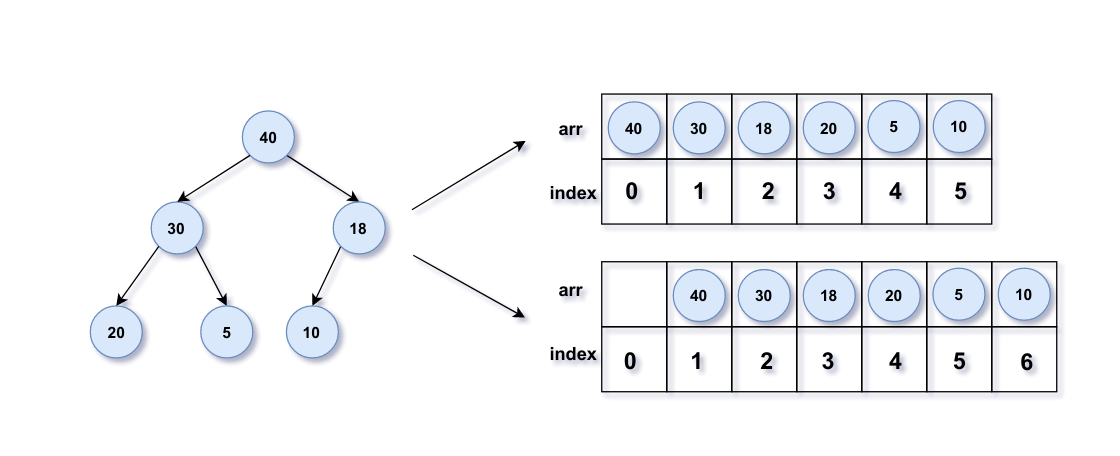
由于用数组描述的二叉堆,堆节点存储在数组中,那么如何用数组表示呢?节点的父子关系又如何解决?i i i l l l r r r
l = 2 i + 1 l=2i+1 l = 2 i + 1 r = 2 i + 2 r=2i+2 r = 2 i + 2 i = ⌊ l − 1 2 ⌋ = ⌊ r − 1 2 ⌋ i=\lfloor \frac{l-1}{2} \rfloor=\lfloor \frac{r-1}{2} \rfloor i = ⌊ 2 l − 1 ⌋ = ⌊ 2 r − 1 ⌋
数组索引从1开始:
l = 2 i l=2i l = 2 i r = 2 i + 1 r=2i+1 r = 2 i + 1 i = ⌊ l 2 ⌋ = ⌊ r 2 ⌋ i=\lfloor \frac{l}{2} \rfloor=\lfloor \frac{r}{2} \rfloor i = ⌊ 2 l ⌋ = ⌊ 2 r ⌋
两者均采用了向下取整floor是防止数组下标越界同时还能保证不同左右孩子的父节点索引相同;数组索引从1开始是为了简化运算,除此之外没有差别,本文是采用第一种方式。
本文仅仅演示最大堆的基本操作,最小堆也是类似的。
template <class T >class Heap {public :virtual void push (const T&) 0 ;virtual int size () 0 ;virtual T& top () 0 ;virtual void pop () 0 ;virtual bool empty () 0 ;virtual ~Heap (){}
从Heap派生出最大堆maxHeap
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 template <class T >class maxHeap :public Heap<T>{public :maxHeap (int init_capacity=20 );maxHeap ();void push (const T& data) void pop () int size () return m_heapSize;}int capacity () return m_capacity;}T& top () {if (m_heapSize>=1 )return m_heap[0 ];throw "heap is empty" ;bool empty () return m_heapSize==0 ;}protected :void changeHeapCapacity (int oldLength,int newLength) new T[newLength];copy (m_heap,m_heap+m_heapSize,temp);delete [] m_heap;private :int m_capacity;int m_heapSize;
最大堆的插入必须要确保每个节点≥ \ge ≥
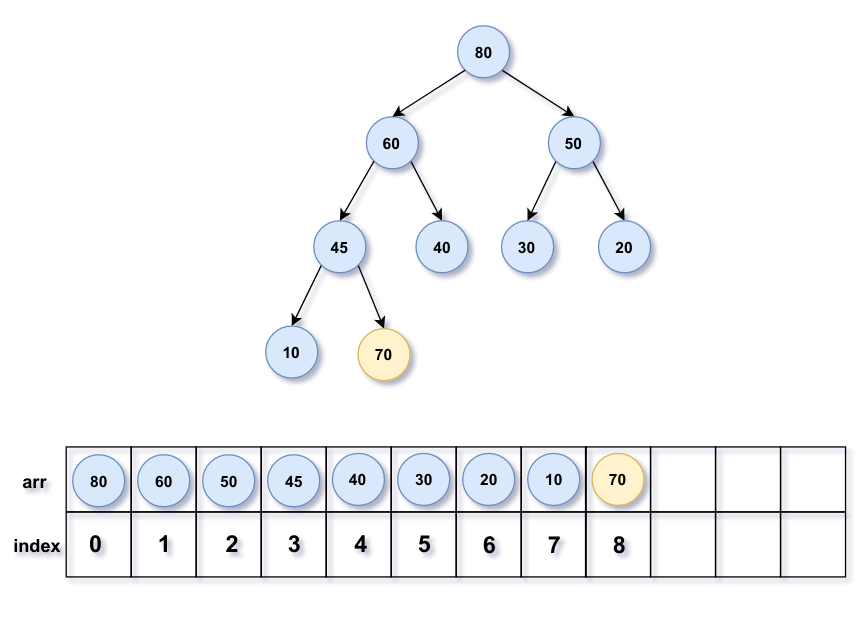
在最大堆的底部最左边添加一个新节点作为子节点,也就是在数组内有效元素的下一个位置插入;
若子节点>父节点,则交换它们的值,继续向上调整;否则调整结束。
二叉堆插入时间复杂度为O ( H e i g h t ) = O ( log n ) O(Height)=O(\log n) O ( H e i g h t ) = O ( log n )
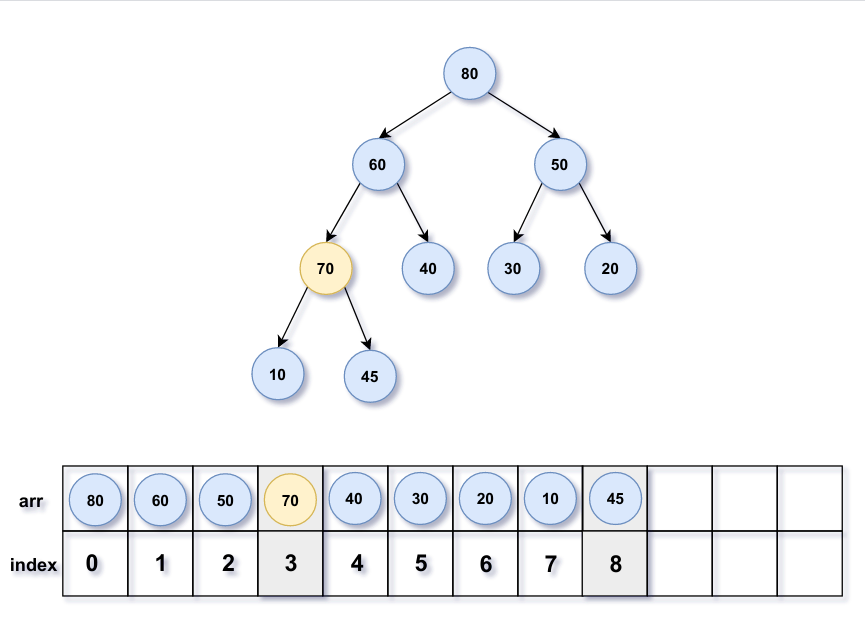
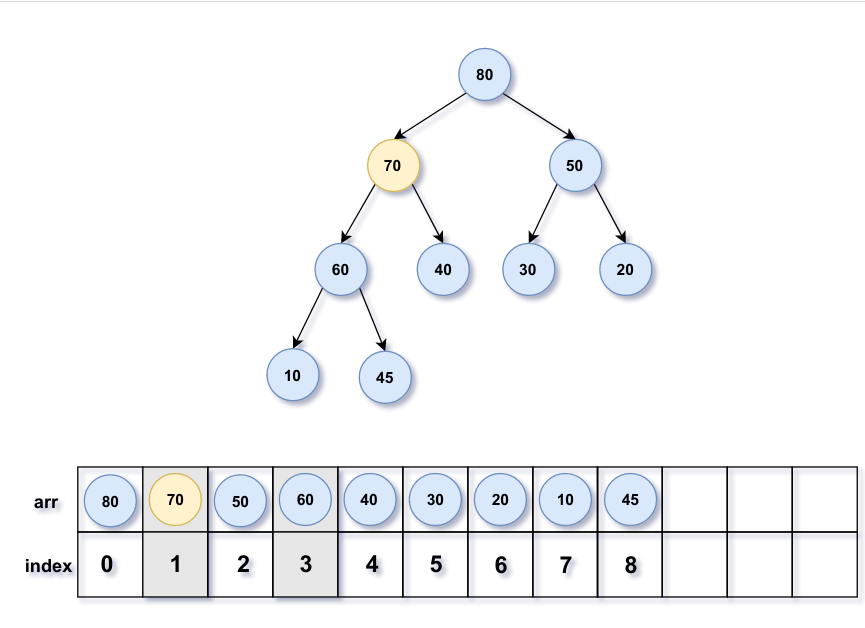
向上调整就像冒泡排序一样,从叶子到根不断将新节点移动到某个位置直到该新节点≤ \le ≤ 节点70在数组中的索引为8,可以计算出父节点45索引为⌊ 8 − 1 2 ⌋ = 3 \lfloor \frac{8-1}{2} \rfloor=3 ⌊ 2 8 − 1 ⌋ = 3 节点70所在数组的索引为3;
接着继续判断节点70和父节点60大小,70>60,继续交换节点70与父节点60的值;此时70<80,调整结束。
如果在空堆中插入节点直接插入即可,注意此处并没有直接交换父节点和子节点,而是将父节点不断的向下移动,最后在合适位置插入新节点。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 template <class T >void maxHeap<T>::push (const T&data){if (m_heapSize>=m_capacity){changeHeapCapacity (m_capacity,2 *m_capacity);int index=m_heapSize;int parent_index=((index-1 )/2 );while (true ) {if (index==0 )break ;if (data > m_heap[parent_index])else break ;-1 )/2 );
一般二叉堆的删除指的是删除堆顶元素,其步骤如下:
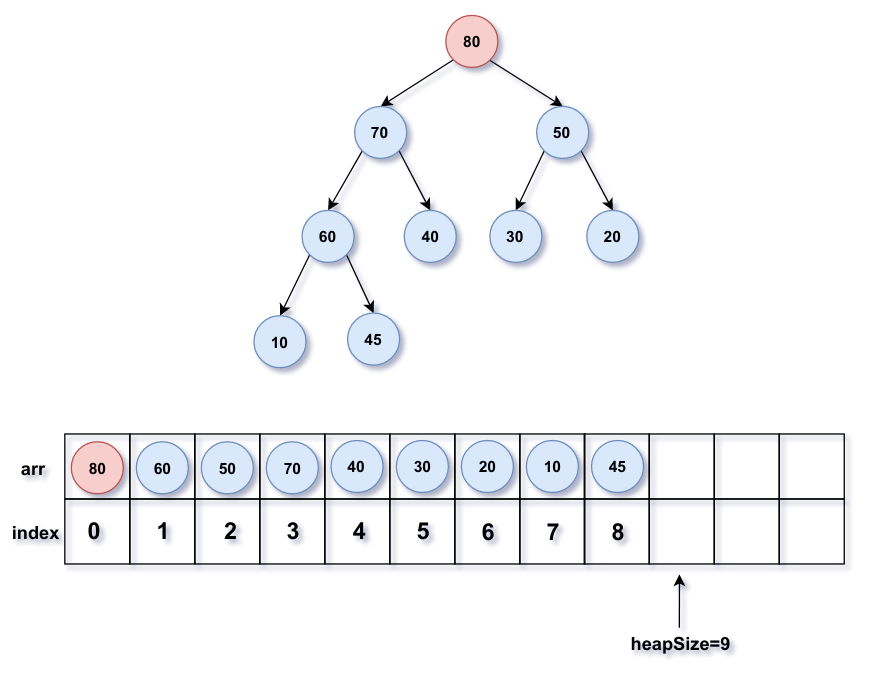
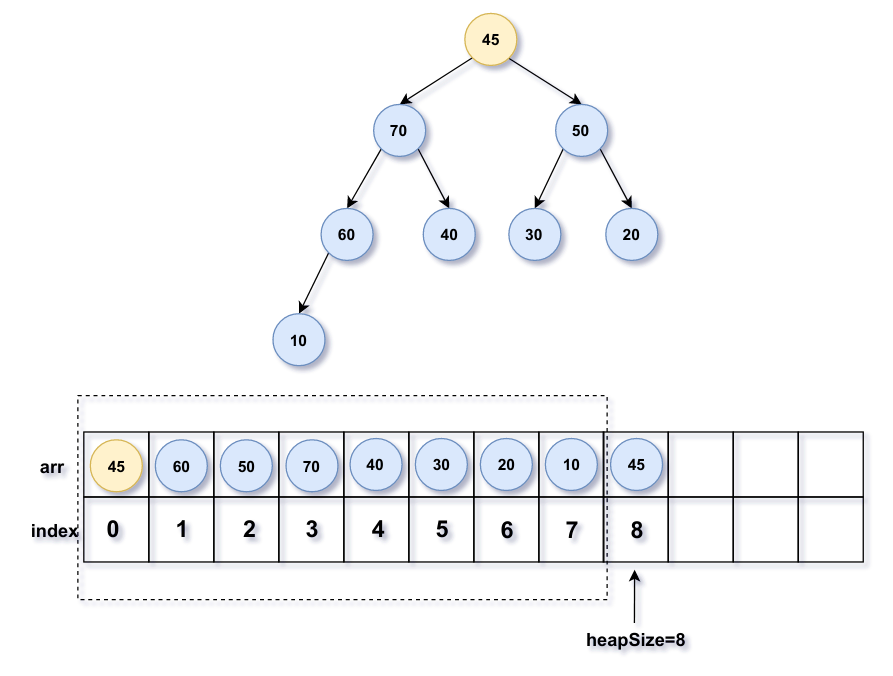
删除堆顶元素并将二叉堆最底层的最后一个节点(数组最后一个元素)替换到堆顶位置(数组第一个元素);
先比较父节点的左右孩子的大小,较大的子节点再与父节点进行比较,若父节点<其子节点,继续向下调整;否则调整结束。
二叉堆删除时间复杂度为O ( H e i g h t ) = O ( log n ) O(Height)=O(\log n) O ( H e i g h t ) = O ( log n )
heapSize-1。
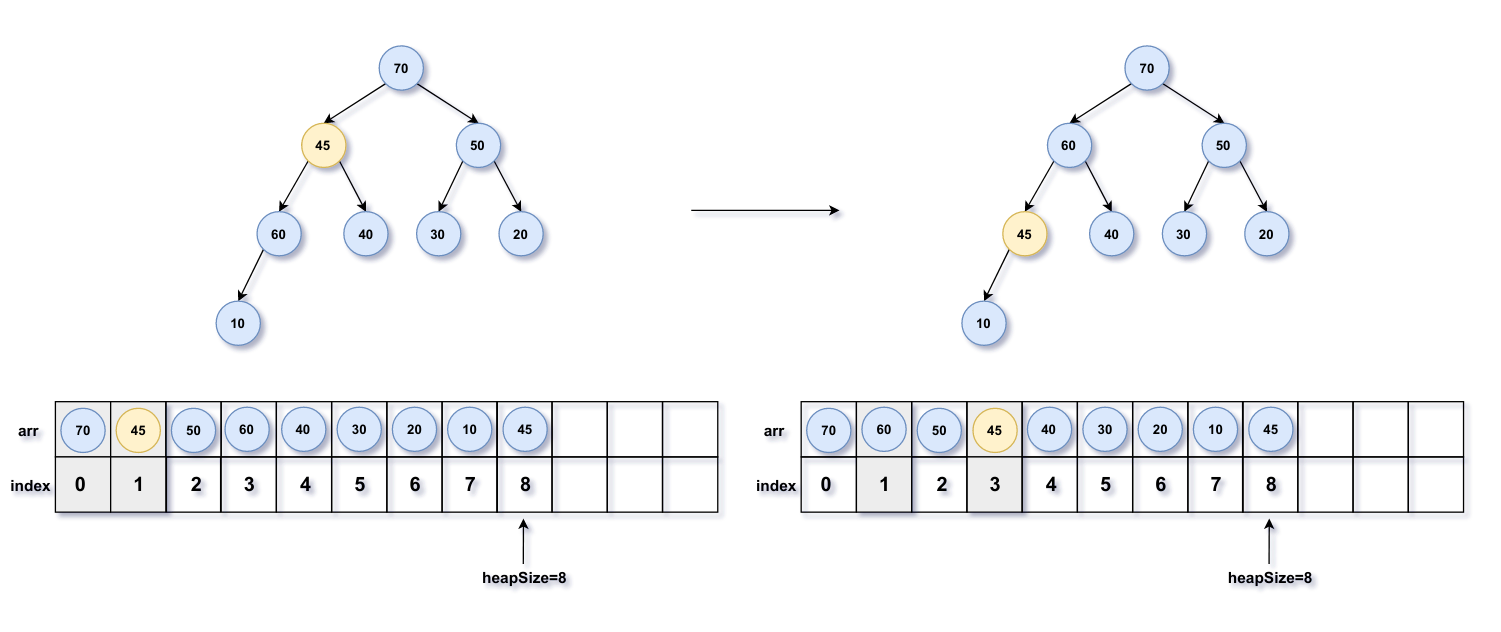
父节点45的左右孩子节点70>50且45<70,故交换值后继续向下调整;
父节点45的左右孩子节点60>40且45<60,故交换值后继续向下调整;
父节点45只有左孩子且45>10,故调整结束。
类似插入操作此处也并没有直接交换父节点和子节点值,而是将子节点不断的向上移动,最后在合适位置插入旧值。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 template <class T >void maxHeap<T>::pop (){if (m_heapSize<=0 )return ;int index=0 ;int child_index=2 *index+1 ;int lastChild=m_heap[--m_heapSize];while (true ){if (child_index >= m_heapSize)break ;if (child_index+1 < m_heapSize && m_heap[child_index]<m_heap[child_index+1 ]){if (lastChild < m_heap[child_index])else break ;2 *index+1 ;
构建二叉堆是在一个循环内不断地插入元素,实际上这是Williams法,其复杂度为O ( n log n ) O(n\log n) O ( n log n )
int array[]={90 , 40 ,30 ,60 ,70 ,200 ,20 ,10 ,50 ,80 };int >mhp;for (auto &&x:array) {push (x);
但是,Williams的方法不够好。事实上,我们可以直接在原数组通过向下调整的方法来建堆,而且这种方法比上面的方法还要快。
More specifically if all the subtrees starting at some height h h h h = 0 h=0 h = 0 h + 1 h+1 h + 1
大概意思是说,如果一个二叉堆的底层子树也是二叉堆的话,那么可以逐层向上合并这些子二叉堆,也就是在h h h h + 1 h+1 h + 1
Build -Max -Heap (A):length [A]for each index i from floor ((length [A]-1 -1 )/2 ) downto 0 do :Max -Heapify(A, i)
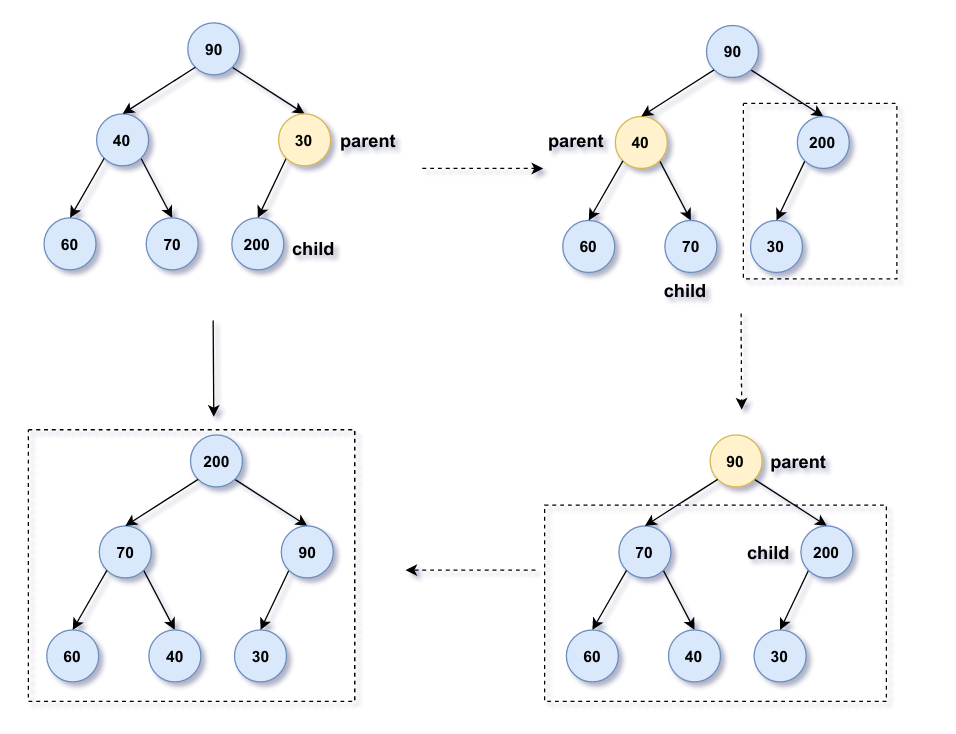
比如下面这张图,数组表示为[90 40 30 60 70 200],这不是一个二叉堆,现在需要将其调整为二叉堆。floor((length[A]-1-1)/2)开始(最后一个子节点的父节点),依次递减直到0(根节点),虚线框表示已经完成堆化的子树。
其中parent代表要下浮的节点,从父节点开始将parent下浮到某个合适位置。最后结果就是真正的二叉堆[200 70 90 60 40 30]。
总之该方法一句话搞定:逐层向上(从右到左,从下到上)的向下调整。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 void buildHeap (T*array,int size) delete []m_heap;for (int i = (size-1 )/2 ; i >=0 ; --i){int index=i;int child_index=2 *index+1 ;while (true ){if (child_index>=size)break ;if (child_index+1 <size&&m_heap[child_index]<m_heap[child_index+1 ])if (parent>=m_heap[child_index])break ;2 +1 ;
虽然该方法复杂度可以说是O ( n log n ) O(n\log n) O ( n log n )
利用最大堆可以对数组升序排序,最小堆可以对数组降序排序。堆排序通过每次“删除”(交换数组首尾元素)堆顶元素(最大/小值),再重新构建二叉堆,使得数组内元素由后往前依次减小,从而数组变得有序。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 void down (int *array,int size,int i) int index=i;int child_index=2 *index+1 ; int x=array[index];while (true ){if (child_index>=size)break ;if (child_index+1 <size&&array[child_index]<array[child_index+1 ])if (x>=array[child_index])break ;2 +1 ;void HeapSort (int *array,int size) int index,child_index,parent,child;for (int i = (size-1 -1 )/2 ; i >=0 ; --i){down (array,size,i);for (int i = size-1 ; i >=0 ; --i){swap (array[i],array[0 ]);down (array,i,0 );