在计算机科学中,树是一种非线性数据结构,树的种类有大致分为两类:无序树和有序树。有序树又分为二叉查找树、堆、左高树、AVL树、红黑树等。树是一种非常重要的数据结构,如C++ STL中的map底层实现原理是红黑树,Java (jdk1.8) HashMap更是采用了散列表+链表+红黑树。
不过在讨论二叉查找树之前,我们需要了解树的一些基本知识。
树
一棵树t是一个非空的有限个元素的集合,其中一个元素为根(root),若其余元素存在,则组成t的子树
如下图图3为仅有一个元素的树,且该元素为树的根(root)
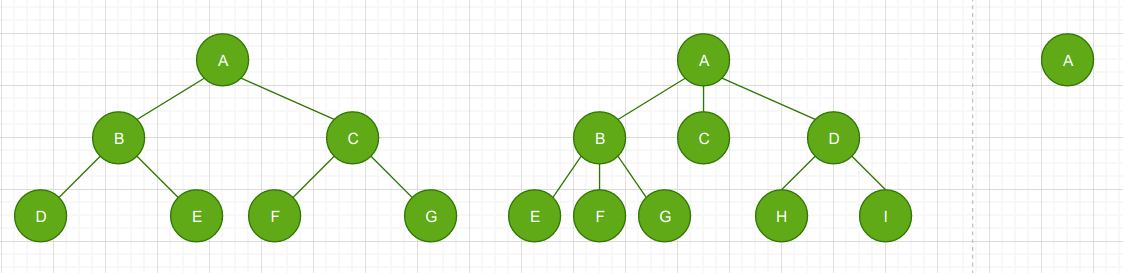
关于树的术语(摘自维基百科)
节点的度:一个节点含有的子树的个数称为该节点的度
树的度:一棵树中,最大的节点度称为树的度
叶节点或终端节点:度为零的节点,也就是没有节点的节点
非终端节点或分支节点:度不为零的节点
父亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点
兄弟节点:具有相同父节点的节点互称为兄弟节点
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推
深度:对于任意节点n,n的深度为从根到n的唯一路径长,根的深度为0
高度:对于任意节点n,n的高度为从n到叶子节点的最长路径长,所有树叶的高度为0
堂兄弟节点:父节点在同一层的节点互为堂兄弟
节点的祖先:从根到该节点所经分支上的所有节点
子孙:以某节点为根的子树中任一节点都称为该节点的子孙
森林:由m(m>=0)棵互不相交的树的集合称为森林
高度和深度的区别其实不用太在意,不同的人有不同的定义。
若有兴趣可以去stackoverflow What is the difference between tree depth and height?
看看
二叉树
定义:一棵二叉树(binary tree) t 是有限个元素的集合(可以为空)。当二叉树非空时,其中一个元素称为根,若存在其余元素,则分为两颗二叉树,分别称为 t 的左子树和右子树
二叉树中每个元素的左子树和右子树是有序的,而树的子树是无序的
性质
二叉树的性质有很多,这里仅列举其中的一些。
性质1:一棵二叉树有n个元素,n>0,它有n−1条边
性质2:一棵二叉树的高度为h,h≥0,它最少有h个元素,最多有2h−1个元素
性质3:一棵二叉树有n个元素,n>0,它的高度最大为n,最小高度为⌈log2(n+1)⌉。
性质4:设完全二叉树其中一个元素编号i,1≤i≤n,则:
- 若i=1,则该元素为二叉树的根。若i>1,则其父节点的编号为 ⌊2i⌋
- 若2i>n,则该元素无左孩子。否则,其左孩子编号2i
- 若2i+1>n,则该元素无右孩子。否则,其右孩子编号2i+1
当高度为h的二叉树恰好有2h−1个元素时,称为满二叉树。
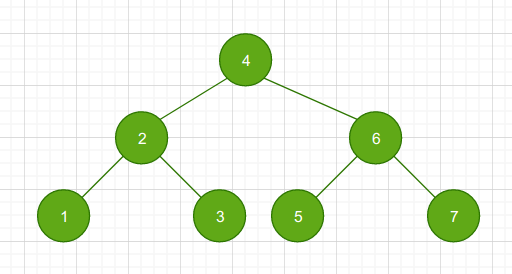
完全二叉树可以看作是满二叉树删除最底层最右边的元素后形成的一棵树。
满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树
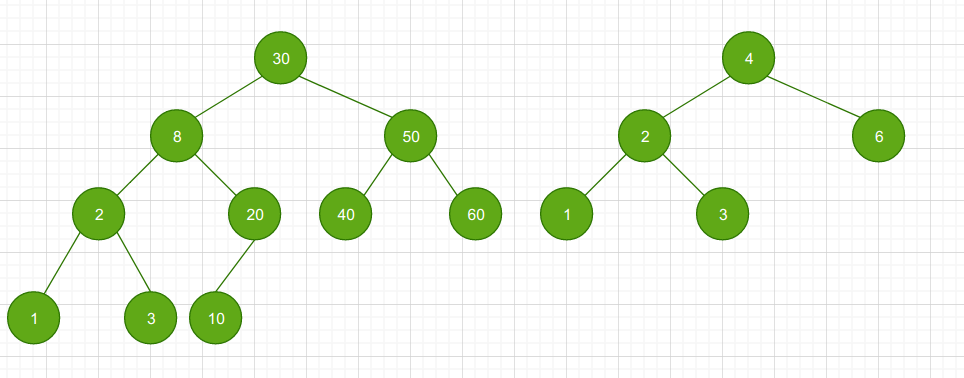
二叉树描述
二叉树描述既可以数组也可以用链表。其中用数组描述的一般是二叉堆,用链表描述的比较常用,适用范围广。因此本文主要是基于链表描述的二叉查找树来展开
二叉查找树(Binary Search Tree)
二叉查找树也可叫做二叉搜索树,其满足以下特征:
- 每个元素有唯一的一个关键字
- 左子树的元素的关键字小于 根节点的关键字
- 右子树的元素的关键字大于 根节点的关键字
- 根节点的左右子树也是二叉查找树

定义一个bst节点结构
| template<typename T>
struct NodeEntry{
int key;
T data;
NodeEntry *parent;
NodeEntry *left_nodes;
NodeEntry *right_nodes;
};
|
bst模板类
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| template<typename T>
class binaryTree
{
public:
typedef T value_type;
typedef T& reference_type;
typedef const T& const_reference_type;
typedef const int& const_key_type;
typedef NodeEntry<T> NODE;
typedef NodeEntry<T>& REF_NODE;
typedef NodeEntry<T>* PNODE;
typedef NodeEntry<T>* & REF_PNODE;
private:
PNODE m_NodeRoot;
public:
binaryTree();
binaryTree(const_key_type k,const_reference_type v);
~binaryTree();
int Height(PNODE pNode);
bool Insert(REF_PNODE pNode,PNODE pNodeParent,const_key_type key,const_reference_type value);
bool Delete(PNODE pNode,const_key_type key);
NodeEntry<T>* Search(PNODE pNode,const_key_type key);
void ClearAll(REF_PNODE pNode);
NodeEntry<T>* predecessor(NODE* pNode);
NodeEntry<T>* successor(NODE* pNode);
void PreOrder(NODE * pRootNode);
void InOrder(NODE * pRootNode);
void PostOrder(NODE * pRootNode);
void LevelOrder(NODE * pRootNode);
};
|
遍历
bst有三种遍历方式
前序遍历
先访问当前节点,然后再遍历左子树,最后遍历右子树
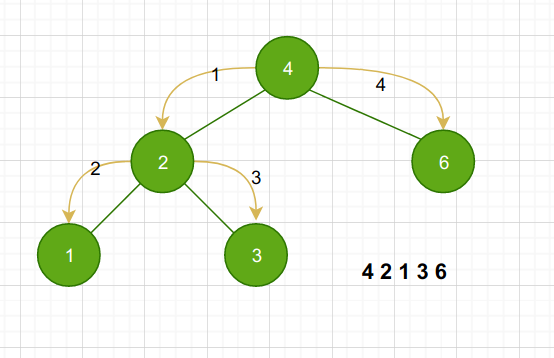
| template<typename T>
void binaryTree<T>::PreOrder(binaryTree::NODE *pRootNode) {
if(pRootNode== nullptr){
return;
}
cout<<pRootNode->key<<endl;
PreOrder(pRootNode->left_nodes);
PreOrder(pRootNode->right_nodes);
}
|
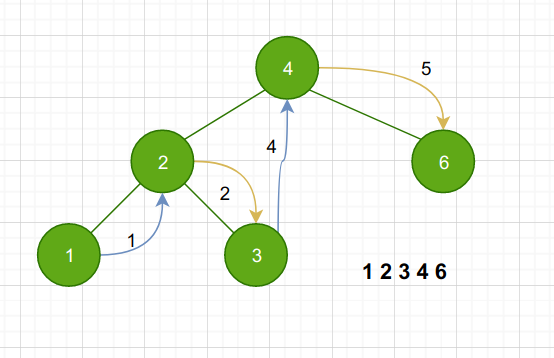
中序遍历
先遍历左子树,再访问当前节点,最后遍历右子树
| template<typename T>
void binaryTree<T>::InOrder(binaryTree::NODE *pRootNode) {
if(pRootNode == nullptr){
return;
}
InOrder(pRootNode->left_nodes);
cout<<pRootNode->key<<endl;
InOrder(pRootNode->right_nodes);
}
|
可见中序遍历能够有序输出节点
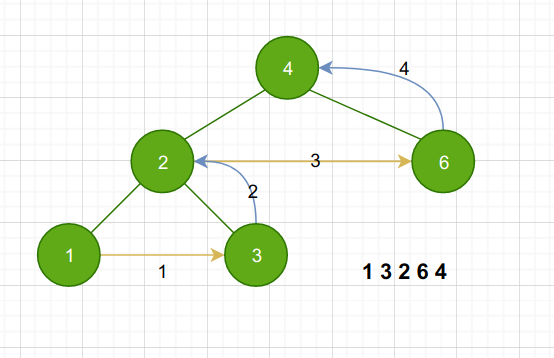
后序遍历
先遍历左子树,再遍历右子树,最后访问当前节点
| void binaryTree<T>::PostOrder(binaryTree::NODE *pRootNode) {
if(pRootNode== nullptr){
return;
}
PostOrder(pRootNode->left_nodes);
PostOrder(pRootNode->right_nodes);
cout<<pRootNode->key<<endl;
}
|
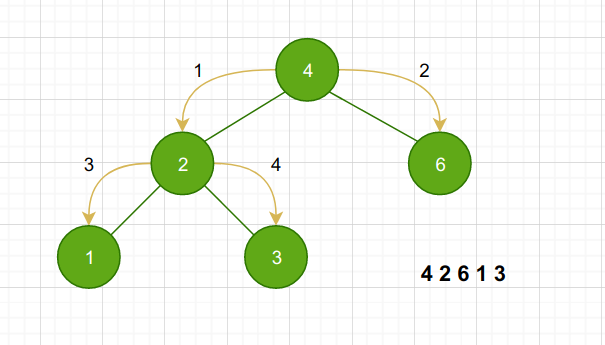
层级遍历
主要是利用广度优先搜索实现的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| template<typename T>
void binaryTree<T>::LevelOrder(binaryTree::NODE *pRootNode) {
if(!pRootNode)return;
queue<binaryTree::PNODE>q;
q.push(pRootNode);
while (!q.empty()){
binaryTree::PNODE pNode=q.front();
cout<<pNode->key<<endl;
if(pNode->left_nodes){
q.push(pNode->left_nodes);
}
if(pNode->right_nodes) {
q.push(pNode->right_nodes);
}
q.pop();
}
}
|
高度
| template<typename T>
int binaryTree<T>::Height(binaryTree::PNODE pNode) {
if(!pNode)return 0;
int h1=Height(pNode->left_nodes);
int h2=Height(pNode->right_nodes);
return std::max(h1,h2)+1;
}
|
查找
bst查找类似二分查找。很简单
| template<typename T>
NodeEntry<T> *binaryTree<T>::Search(PNODE pNode,const_key_type key) {
if(!pNode)return nullptr;
if(pNode->key==key){
return pNode;
}else if(key<pNode->key){
return Search(pNode->left_nodes,key);
}else if(key>pNode->key){
return Search(pNode->right_nodes,key);
}
return nullptr;
}
|
前驱/后继节点
要完成bst的删除操作,那么就必须要知道前驱/后继节点怎么找。
前驱节点: 假设存在一个节点N,那么它的前驱节点就是关键字小于N的且最大的节点。即key[max(predecessor)]<key[N]
后继节点: 假设存在一个节点N,那么它的后继节点就是关键字大于N的且最小的节点。即key[min(successor)]>key[N]
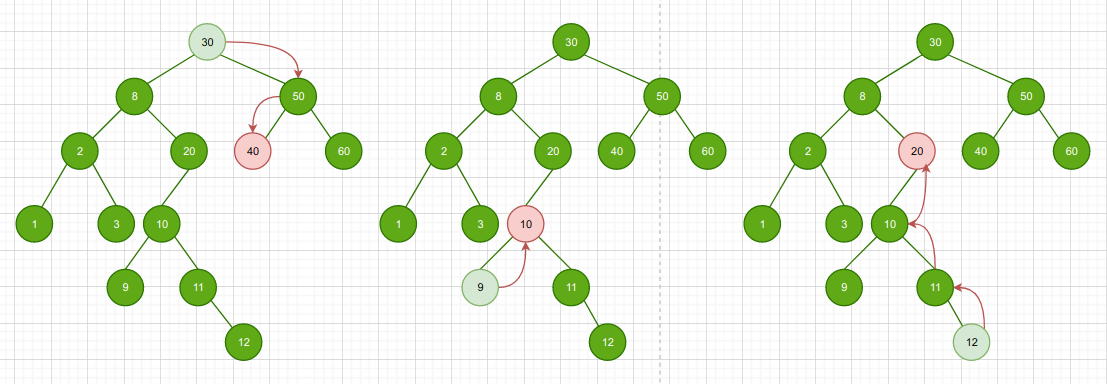
根据前驱节点定义查找:
- 若节点N有左子树L:且左子树L的右子树存在,则依次遍历L的右子树直到叶子节点,就是前驱节点;否则该左子树L就是前驱节点
- 若节点N无左子树,但节点N是其父节点P的右孩子,那么父节点P就是该节点N的前驱结点
- 若节点N无左子树,但该节点N是其父节点P的左孩子,那么需要沿着父亲节点P一直向树的顶端寻找,直到找到一个节点X是其父节点M的右孩子,则节点M为前驱节点
以上三种情况分别对应下图
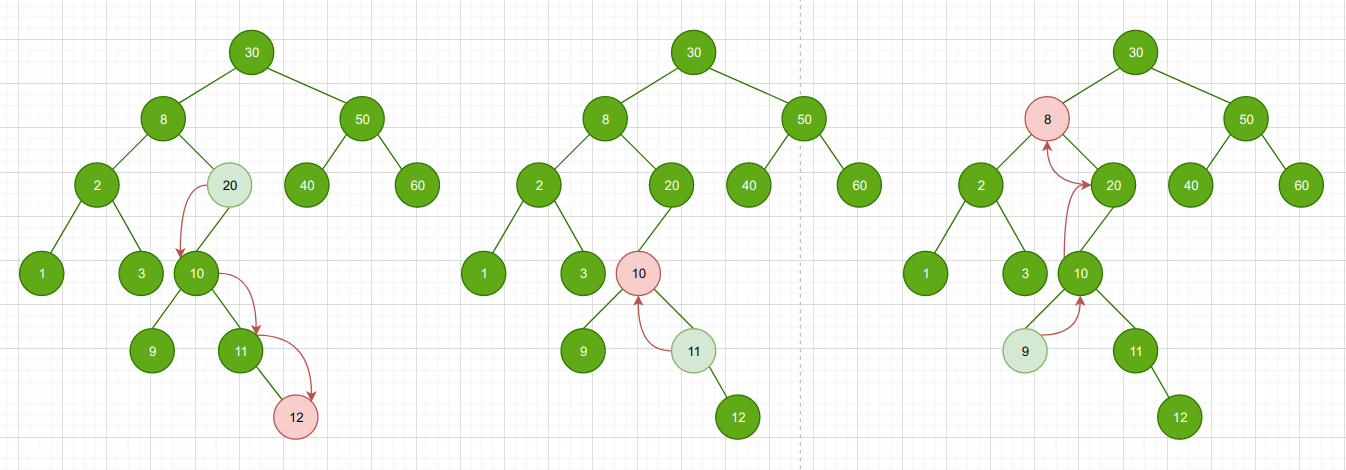
后继节点查找类似前驱节点
- 若节点N有右子树R:且右子树R的左子树存在,则依次遍历R的左子树直到叶子节点,就是后继节点;否则该右子树R就是后继节点
- 若节点N无右子树,但节点N是其父节点P的左孩子,那么父节点P就是该节点N的后继结点
- 若节点N无右子树,但该节点N是其父节点P的右孩子,那么需要沿着父亲节点P一直向树的顶端寻找,直到找到一个节点X是其父节点M的左孩子,则节点M为后继节点
代码如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
| template<typename T>
NodeEntry<T>* binaryTree<T>::predecessor(NODE* pNode)
{
if(!pNode)return nullptr;
if (pNode->left_nodes){
auto x=pNode->left_nodes;
while (x->right_nodes){
x=x->right_nodes;
}
return x;
}else if(pNode->parent){
if (pNode->parent->right_nodes==pNode){
return pNode->parent;
}else{
NodeEntry<T>* parent=pNode->parent;
while (parent && parent->left_nodes==pNode){
pNode=parent;
parent=parent->parent;
}
return parent;
}
}
return nullptr;
}
template<typename T>
NodeEntry<T>* binaryTree<T>::successor(NODE* pNode)
{
if(!pNode)return nullptr;
if (pNode->right_nodes){
auto x=pNode->right_nodes;
while (x->left_nodes){
x=x->left_nodes;
}
return x;
}else if(pNode->parent){
if (pNode->parent->left_nodes==pNode){
return pNode->parent;
}else{
NodeEntry<T>* parent=pNode->parent;
while (parent && parent->right_nodes==pNode){
pNode=parent;
parent=parent->parent;
}
return parent;
}
}
return nullptr;
}
|
插入
讲完前驱后继的查找后,接下来是插入操作,bst的插入比较简单,也就是在空节点nullptr处更新一个新节点,插入方法类似查找方法。插入操作要保证key的唯一性
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| template<typename T>
bool binaryTree<T>::Insert(REF_PNODE pNode,PNODE pNodeParent,const_key_type key,const_reference_type value) {
if(pNode == nullptr){
pNode=new NODE();
pNode->key=key;
pNode->left_nodes= nullptr;
pNode->right_nodes= nullptr;
pNode->data=value;
pNode->parent=pNodeParent;
return true;
}
else if(key < pNode->key){
return Insert(pNode->left_nodes,pNode,key,value);
}
else if(key > pNode->key){
return Insert(pNode->right_nodes,pNode,key,value);
}
else{
cout<<"Already exist!"<<endl;
return false;
}
}
|
删除
删除操作就有点复杂了,不过照着思路也很容易写出来。
大致分为三类
- 删除叶子结点
- 删除只有一棵子树的节点
- 删除有两棵子树的节点
注意:删除操作一定要维护二叉查找树的性质!!!
删除叶子结点,这类情况最为简单,找到待删除节点后直接delete,同时更新父子节点关系;
删除有两棵子树的节点的操作可以转化为删除只有一棵子树的节点,转化策略有前驱和后继两种,本文删除节点使用的策略为后继法。
首先来看一下这个例子
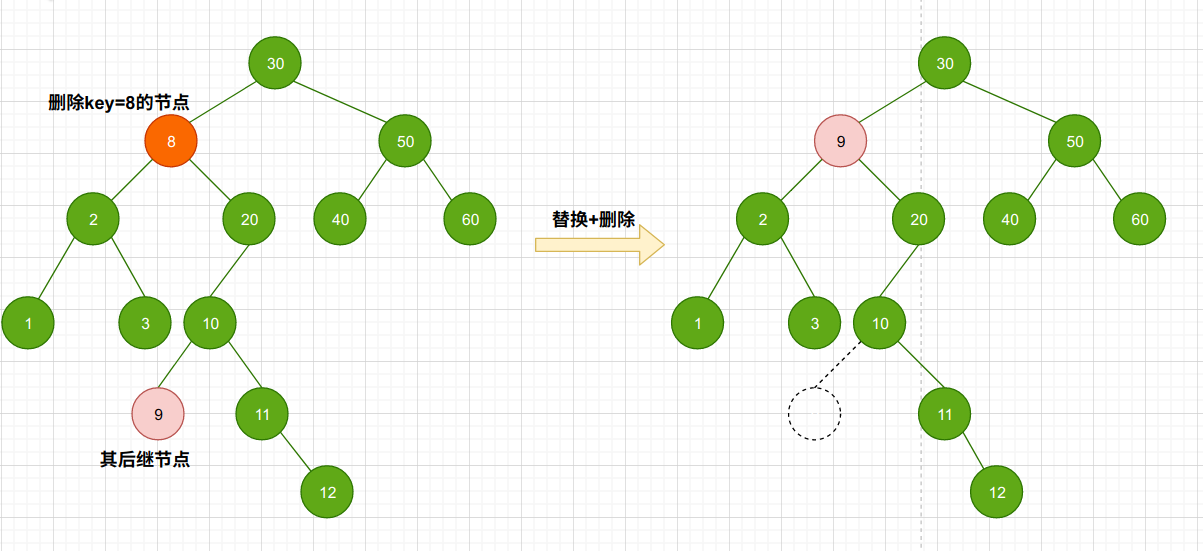
删除key=8的节点,不一定真的是删除该节点,不然的话还要重新建立父子节点关系以及维护bst的性质。因此,利用前驱/后继节点的方法可以巧妙的避开这些不必要的麻烦:只需要替换待删除节点和前驱/后继节点的数据,然后利用删除只有一棵子树的节点的方法来删除前驱/后继节点即可。
删除只有一棵子树的节点情况如下
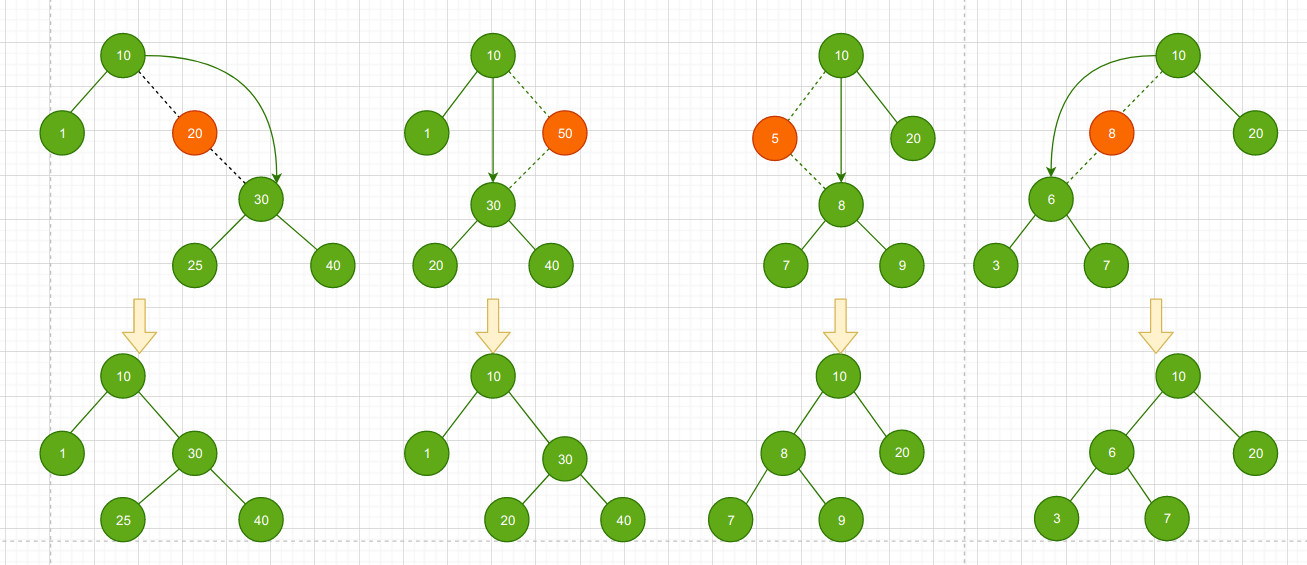
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
| template<class T>
bool binaryTree<T>::Delete(PNODE pNode,const_key_type key) {
PNODE pDeletenode = this->Search(pNode,key);
if(!pDeletenode) return false;
if(pDeletenode->left_nodes!=nullptr&&pDeletenode->right_nodes!=nullptr){
PNODE successor=this->successor(pDeletenode);
pDeletenode->key=successor->key;
pDeletenode->data=successor->data;
pDeletenode=successor;
}
PNODE child=nullptr;
if(pDeletenode->left_nodes!=nullptr){
child=pDeletenode->left_nodes;
}else{
child=pDeletenode->right_nodes;
}
if(child!=nullptr){
child->parent=pDeletenode->parent;
}
if(pDeletenode->parent==nullptr){
m_NodeRoot=child;
}else if(pDeletenode->parent->left_nodes==pDeletenode){
pDeletenode->parent->left_nodes=child;
}else{
pDeletenode->parent->right_nodes=child;
}
delete pDeletenode;
pDeletenode=nullptr;
return true;
}
|
bst释放
递归方式释放所有节点
| template<typename T>
void binaryTree<T>::ClearAll(binaryTree::REF_PNODE pNode) {
if(!pNode)return;
ClearAll(pNode->left_nodes);
ClearAll(pNode->right_nodes);
delete pNode;
pNode= nullptr;
}
|
ok,基本上bst大致讲完了,bye~











