数据结构-C++链表实现

最近在研究《数据结构、算法与应用C++语言描述》，把一些自己的看法和代码实现写在这里，算是个记录吧，以免以后忘记。

线性表——链表描述

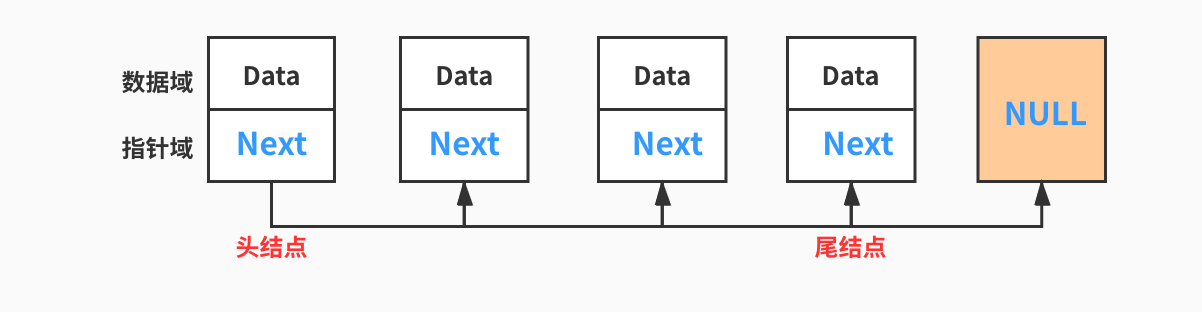
总所周知，数组中元素地址在内存中是连续分布的，而链表的元素在内存中的存储位置是随机的。其中比较简单的链表类型就是单向链表，这种类型的链表的每个节点只有一个链，且每个节点都连接下一个节点（除了最后一个节点:NULL用来标记链表的结束）。

为了用链表描述线性表，需要定义一个节点结构体，使用C++模板能够支持更多的类型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
template<class T>
struct chainNode{
    T data;
    chainNode* next;
    chainNode(){}
    chainNode(const T &data){
        this->data=data;
        this->next=nullptr;
    }
    chainNode(const T &data,chainNode*next){
        this->data=data;
        this->next=next;
    }
};

链表类LinkedList

我们需要定义一个类，用于管理链表操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
template<class T>
class LinkedList{
protected:
    chainNode<T>*m_Header;
    int m_size;
public:
    LinkedList();
    LinkedList(const T&);
    // 拷贝构造函数
    LinkedList(const LinkedList<T>&);
    // 移动构造函数
    LinkedList(LinkedList<T>&&);
    virtual ~LinkedList();
    // 插入节点
    void insert(int,const T&);
    // 在链表尾插入节点
    void append(const T&);
    // 删除指定索引的节点
    void eraseByIndex(int);
    // 删除所有元素为T的节点
    void erase(const T&);
    // 删除所有节点
    void clearAll();
    bool empty();
    int size();
    // 返回首次出现的节点索引
    int indexOf(const T&);
    T &get(int);
    chainNode<T>*getFirstchainNode();
    chainNode<T>*getLastchainNode();
    // 输出所有节点
    void outputLinkedList();
};

插入节点

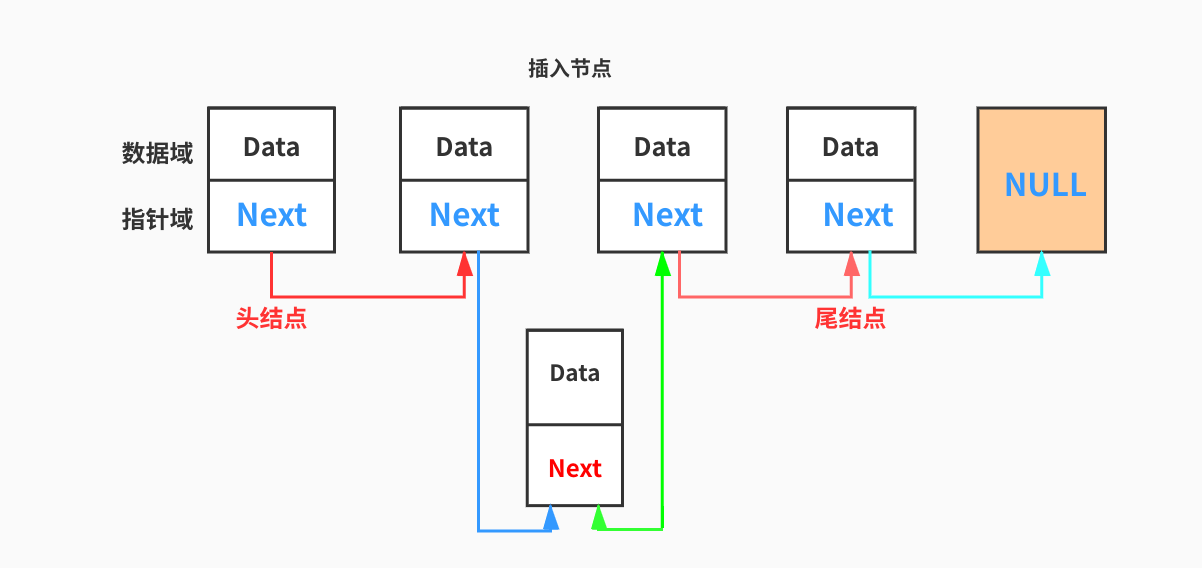
链表的插入其实很简单，首先需要找到索引index的节点，然后在该节点之后或者之前插入新元素节点，那么？如何插入呢？其实就是通过 chainNode* next 指针将内存中的节点地址链接起来，chainNode* next 也只是一个变量标识符来标识内存中的地址罢了，因此我们可以通过替换next指针将需要插入的节点和已经存在的链表串起来，如下图所示

为了说明，我们先来一个最简单的例子，在链表尾处插入节点

append()

代码如下

1
2
3
4
5
6
7
8
9
template<class T>
void LinkedList<T>::append(const T&data){
    chainNode<T>*pNode=m_Header;
    while (pNode->next){
        pNode=pNode->next;   
    }
    pNode->next=new chainNode<T>(data);
    this->m_size++;
}

要在尾部插入节点，那么需要单向遍历整个链表，注意 while (pNode->next) 不能是 while (pNode) ，因为我们需要用尾节点添加一个新节点，同时更新链表大小

注意：可能有人会有疑惑：pNode=pNode->next 会让m_Header 指向下一个节点啊？其实 chainNode*pNode=m_Header;  只是将 m_Header 的地址值复制给pNode变量而已，虽然pNode会修改其地址值，但是它内存中的数据对象没有改变，改变的只是一个普通的指针变量

insert()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
template<class T>
void LinkedList<T>::insert(int theIndex,const T&data){
    if(theIndex<0||theIndex>=m_size)return;    
    // 新建头节点
    if(theIndex==0 && m_Header==nullptr){
        m_Header=new chainNode<T>(data);
        m_size++;
    }else{
        chainNode<T>*pNode=m_Header;
        int index=0;
        while (pNode){
            // 在 theIndex之后 插入节点
            // 找到了要插入的索引
            if(index==theIndex){
                // 新节点
                pNode->next=new chainNode<T>(data,pNode->next);
                // 该语句等同于: 即替换next指针，使其衔接起来
                // auto p=new chainNode<T>(data);
                // p->next=pNode->next;
                // pNode->next=p;
                m_size++;
            }
            index++;
            // 指向下一个节点
            pNode=pNode->next;
        }
    }
}

输出链表节点

在介绍删除之前，我们需要输出链表节点内容方便调试，这段代码很简单，基本都是while(pNode)循环的套路

1
2
3
4
5
6
7
8
9
10
11
template<class T>
void LinkedList<T>::outputLinkedList(){
    if(this->m_Header==nullptr)return;
    chainNode<T>*pNode=this->m_Header;
    int index=0;
    while (pNode){
        std::cout<<"["<<index<<"] => "<<pNode->data<<std::endl;
        index++;
        pNode=pNode->next;
    }
}

删除节点

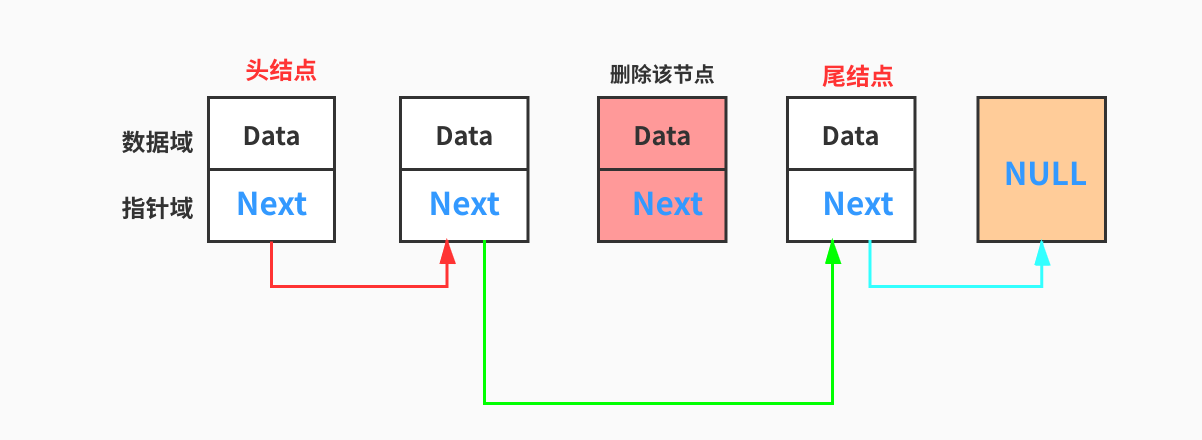
删除链表中的某个节点类似于插入节点，也是通过指针替换的手段，然后delete掉要删除的节点即可。不过有些地方需要注意。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
template<class T>
void LinkedList<T>::eraseByIndex(int theIndex){
    if(theIndex<0 || theIndex>=m_size)return;  
    // deletedNode 为待删除节点
    chainNode<T>*deletedNode=nullptr;
    // 处理删除头节点特殊情况，因为单向链表头结点无前驱节点
    if(theIndex==0){
        // 将 m_Header 标记为删除
        deletedNode = m_Header;
        // 更新头节点
        m_Header=m_Header->next;
    }
    else{
        // 其他情况
        chainNode<T>*pNodePre=m_Header;
        // 查找 待删除节点的前驱节点，其索引为theIndex-1
        for (int i = 0; i < theIndex-1; i++){
            pNodePre=pNodePre->next;   
        }
        // 指针替换
        deletedNode=pNodePre->next;
        pNodePre->next=deletedNode->next;
    }
    // 删除节点
    delete deletedNode;
    deletedNode=nullptr;
    m_size--;
}

其中要注意如果要删除索引为0的节点也就是头结点，那么只需要让头结点更新为原来的下一个节点，然后再delete要删除的节点，这种情况很特殊，因为单向链表头结点无前驱节点。其他情况需要一个前驱节点（也就是当前节点的上一个节点）来衔接整个链表。

再来看下面的代码，删除链表中所有数据为data的节点，同时还处理的头结点的特殊情况

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
template<class T>
void LinkedList<T>::erase(const T&data){
    chainNode<T>*pNode=m_Header;
    chainNode<T>*pNodePre;
    while (pNode){
        if(pNode->data==data){
            // 处理删除头结点情况
            if(pNode==m_Header){
                auto next=m_Header->next;
                delete m_Header;
                m_Header=next;
                // 并使其指向原来头结点的下一个节点
                pNode=next;
                m_size--;
            }
            else{
                pNodePre->next=pNode->next;
                delete pNode;
                // 这条语句能够继续删除链表中数据为data的节点
                pNode=pNodePre;
                m_size--;
            }
        }
        // 保存前驱节点
        pNodePre=pNode;
        pNode=pNode->next;
    }
}

其他成员函数

事实上，当真正了解的单向链表的插入删除的本质时，其他的链表类型也能理解。

单向链表是最基础的一种链表类型，当然还有其他的一些变种：循环列表、双向链表、双向循环链表、甚至是树结构（层次结构 ）也与链表密不可分。因此，必须要对链表十分熟悉！！！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

template<class T>
bool LinkedList<T>::empty(){
    return this->m_Header==nullptr&&this->m_size<=0;
}
template<class T>
int LinkedList<T>::size(){
    return this->m_size;
}

template<class T>
int LinkedList<T>::indexOf(const T&data){
    chainNode<T>*pNode=m_Header;
    int index=0;
    while (pNode&&pNode->data!=data){
        index++;
        pNode=pNode->next;
    }
    // 到达链表尾pNode标识为nullptr，表示没有找到
    if(pNode==nullptr)
        return -1;
    else
        return index;    
}
template<class T>
T &LinkedList<T>::get(int index){
    if(index<0 || index>=m_size)
        throw length_error("the index is invalid!");
    chainNode<T>*pNode=m_Header;
    int count=0;
    while (pNode&&index!=(count++)){
        pNode=pNode->next;
    }
    return pNode->data;
}
template<class T>
chainNode<T>* LinkedList<T>::getFirstchainNode(){
    return m_Header;
}
template<class T>
chainNode<T>* LinkedList<T>::getLastchainNode(){
    auto p=m_Header;
    while (p&&p->next){
        p=p->next;   
    }
    return p;
}

完整代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
#pragma once
#include<iostream>
using namespace std;

template<class T>
struct chainNode{
    T data;
    chainNode* next;
    chainNode(){}
    chainNode(const T &data){
        this->data=data;
        this->next=nullptr;
    }
    chainNode(const T &data,chainNode*next){
        this->data=data;
        this->next=next;
    }
};
template<class T>
class LinkedList{
protected:
    chainNode<T>*m_Header;
    int m_size;
public:
    LinkedList();
    LinkedList(const T&);
    // 拷贝构造函数
    LinkedList(const LinkedList<T>&);
    // 移动构造函数
    LinkedList(LinkedList<T>&&);
    virtual ~LinkedList();
    
    void insert(int,const T&);
    void append(const T&);
    void eraseByIndex(int);
    // 删除所有元素为T的节点
    void erase(const T&);
    void clearAll();
    bool empty();
    int size();
    // 返回首次出现的节点索引
    int indexOf(const T&);
    T &get(int);
    chainNode<T>*getFirstchainNode();
    chainNode<T>*getLastchainNode();
    void outputLinkedList();
};

template<class T>
LinkedList<T>::LinkedList(){
    m_Header=nullptr;
    m_size=0;
}

template<class T>
LinkedList<T>::LinkedList(const T&data){
    m_Header=new chainNode<T>(data);
    m_size=1;
}
// 拷贝构造函数->深拷贝
template<class T>
LinkedList<T>::LinkedList(const LinkedList<T>&ll){
    if(ll.m_Header==nullptr)
        throw runtime_error("The source object can not nullptr!");
    this->m_size=ll.m_size;
    // 构建头节点
    this->m_Header=new chainNode<T>(ll.m_Header->data);
    chainNode<T>*pNodeSource=ll.m_Header->next;
    chainNode<T>*pNodeTarget=this->m_Header;
    // 从源链表的头结点的下一个节点开始逐个复制
    while (pNodeSource){
        pNodeTarget->next=new chainNode<T>(pNodeSource->data);
        pNodeSource=pNodeSource->next;
        pNodeTarget=pNodeTarget->next;
    }
    pNodeTarget->next=nullptr;
}

// 移动构造函数->浅拷贝
template<class T>
LinkedList<T>::LinkedList(LinkedList<T>&&ll){
    this->m_size=ll.m_size;
    this->m_Header=ll.m_Header;
    // 禁止内存区域共享
    ll.m_Header=nullptr;
}

template<class T>
LinkedList<T>::~LinkedList(){
    if(this->m_Header){
        this->clearAll();
    }
}
template<class T>
void LinkedList<T>::insert(int theIndex,const T&data){
    if(theIndex<0||theIndex>=m_size)return;    
    // 新建头节点
    if(theIndex==0&&m_Header==nullptr){
        m_Header=new chainNode<T>(data);
        m_size++;
    }else{
        chainNode<T>*pNode=m_Header;
        int index=0;
        while (pNode){
            // 在 theIndex之后 插入节点
            if(index==theIndex){
                pNode->next=new chainNode<T>(data,pNode->next);
				// auto p=new chainNode<T>(data);
                // p->next=pNode->next;
                // pNode->next=p;
                m_size++;
            }
            index++;
            pNode=pNode->next;
        }
    }
}
template<class T>
void LinkedList<T>::append(const T&data){
    chainNode<T>*pNode=m_Header;
    while (pNode->next){
        pNode=pNode->next;   
    }
    pNode->next=new chainNode<T>(data);
    this->m_size++;
}   

template<class T>
void LinkedList<T>::clearAll(){
    while (m_Header){
        chainNode<T>*pNextNode=m_Header->next;
        delete m_Header;
        m_Header=nullptr;
        m_Header=pNextNode;
    }
    m_Header=nullptr;
    m_size=0;
}

template<class T>
void LinkedList<T>::eraseByIndex(int theIndex){
    if(theIndex<0||theIndex>=m_size)return;    
    chainNode<T>*deletedNode=nullptr;
    // 处理删除头节点情况，因为单向链表头结点无前驱节点
    if(theIndex==0){
        // 将 m_Header 标记为删除
        deletedNode = m_Header;
        m_Header=m_Header->next;
    }
    else{
        chainNode<T>*pNodePre=m_Header;
        // 找待删除节点的前驱节点
        for (int i = 0; i < theIndex-1; i++){
            pNodePre=pNodePre->next;   
        }
        deletedNode=pNodePre->next;
        pNodePre->next=deletedNode->next;
    }
    delete deletedNode;
    deletedNode=nullptr;
    m_size--;
}

template<class T>
void LinkedList<T>::erase(const T&data){
    chainNode<T>*pNode=m_Header;
    chainNode<T>*pNodePre;
    while (pNode){
        if(pNode->data==data){
            // 处理删除头结点情况
            if(pNode==m_Header){
                auto next=m_Header->next;
                delete m_Header;
                m_Header=next;
                // 并使其指向原来头结点的下一个节点
                pNode=next;
                m_size--;
            }
            else{
                pNodePre->next=pNode->next;
                delete pNode;
                pNode=pNodePre;
                m_size--;
            }
        }
        // 保存前驱节点
        pNodePre=pNode;
        pNode=pNode->next;
    }
}
template<class T>
bool LinkedList<T>::empty(){
    return this->m_Header==nullptr&&this->m_size<=0;
}
template<class T>
int LinkedList<T>::size(){
    return this->m_size;
}

template<class T>
int LinkedList<T>::indexOf(const T&data){
    chainNode<T>*pNode=m_Header;
    int index=0;
    while (pNode&&pNode->data!=data){
        index++;
        pNode=pNode->next;
    }
    // 到达尾节点
    if(pNode==nullptr)
        return -1;
    else
        return index;    
}
template<class T>
T &LinkedList<T>::get(int index){
    if(index<0||index>=m_size)
        throw length_error("the index is invalid!");
    chainNode<T>*pNode=m_Header;
    int count=0;
    while (pNode&&index!=count++){
        pNode=pNode->next;
    }
    return pNode->data;
}
template<class T>
chainNode<T>* LinkedList<T>::getFirstchainNode(){
    return m_Header;
}
template<class T>
chainNode<T>* LinkedList<T>::getLastchainNode(){
    auto p=m_Header;
    while (p&&p->next){
        p=p->next;   
    }
    return p;
}

template<class T>
void LinkedList<T>::outputLinkedList(){
    if(this->m_Header==nullptr)return;
    chainNode<T>*pNode=this->m_Header;
    int index=0;
    while (pNode){
        std::cout<<"["<<index<<"] => "<<pNode->data<<std::endl;
        index++;
        pNode=pNode->next;
    }
}

有序链表

其实我们还可以利用上面的单向链表实现一个简单的有序链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

#pragma once
#include"LinkedList.h"

// 默认升序
template<class T,class Compare=less<T>>
class SortedLinkedList: public LinkedList<T> {
public: 
    using LinkedList<T>::LinkedList;
    using LinkedList<T>::insert;
    ~SortedLinkedList(){}
    // 子类insert为有序插入
    void insert(const T&);
    // 基类insert为无序插入
};
// 重载insert()函数
template<class T,class Compare>
void SortedLinkedList<T,Compare>::insert(const T&data){
    chainNode<T>*pNode=this->m_Header;
    chainNode<T>*pNodePre=nullptr;
    // Compare()(pNode->data,data) 等价于 pNode->data < data
    // 找前驱节点
    while (pNode&&Compare()(pNode->data,data)){
        pNodePre=pNode;
        pNode=pNode->next;
    }
    // 若无前驱节点，那么没有头结点 或者 pNode->data > data
    if(pNodePre==nullptr){
        // 更新头结点
        this->m_Header=new chainNode<T>(data,pNode);
        // 等价于
        // auto p=new chainNode<T>(data);
        // p->next=pNode; 
        // this->m_Header=p;
    }
    else{
        // 插入新节点
        chainNode<T>*p=new chainNode<T>(data,pNode);
        pNodePre->next=p;
        // 等价于
        // auto p=new chainNode<T>(data);
        // p->next=pNode;
        // pNodePre->next=p;
    }
    this->m_size++;
}

结尾

链表元素在内存随机存储的，占用一定的内存空间，且查找速度要慢于顺序表，但在插入和删除方面要优于顺序表。如果有一种数据结构够将两者结合起来，那么就能够充分利用两者的优点，这种数据结构就是跳表和散列表。