本文选自算法导论某一章节，并用高等数学知识对其进行总结

线段

探讨的问题：

• 对于给定的两个有向线段 $\vec{p_0p_1}$ 和 $\vec{p_0p_2}$ ，相对于他们的公共端点 $p_0$ 来说，$\vec{P_0p_1}$ 是否在 $\vec{p_0p_2}$ 的顺时针方向？
• 对于给定的两个线段 $\overline{p_0p_1}$ 和 $\overline{p_0p_2}$ ，如果先沿着 $\overline{p_0p_1}$ 再沿着 $\overline{p_0p_2}$ 前进，那么在点 $p_1$ 处是否要向左转？
• 线段 $\overline{p_0p_1}$ 和 $\overline{p_0p_2}$ 是否相交？

向量积

向量积是计算线段的核心方法。若仅考虑二维平面 $(xOy)$，对于给定的向量 $p_1=(x_1,y_1，0)$ 和 $p_2=(x_2,y_2，0)$ ，则：

$p_1\times p_2= \begin{gathered} \begin{bmatrix} \vec{i} & \vec{j} & \vec{k}\\ x_1 & y_1 & 0\\ x_2 & y_2 & 0 \end{bmatrix} \quad =\begin{bmatrix} x_1 & y_1\\ x_2 & y_2 \end{bmatrix}\cdot \vec{k} =(x_1y_2-x_2y_1)\cdot \vec{k} \end{gathered}$

若将向量看作大小运算，则：

$p_1\times p_2=x_1y_2-x_2y_1=-p_2\times p_1$

• 若 $p_1\times p_2$ 为正，则相对于 原点$(0,0)$ 来说， $p_1$ 位于 $p_2$ 的顺时针方向；
• 若 $p_1\times p_2$ 为负，则相对于 原点$(0,0)$ 来说， $p_1$ 位于 $p_2$ 的逆时针方向；
• 若 $p_1\times p_2$ 为零，则表示出现边界情况，此时两个向量是共线的

为了确定相对于公共端点 $p_0$ ，有向线段 $\vec{p_0p_1}$ 是在顺时针还是逆时针方向更靠近 $\vec{p_0p_1}$，可以将 $p_0$ 作为原点简化问题：用 $p_1-p_0$ 表示向量 $p'_1=(x_1-x_0,y_1-y_0)$ 和 $p'_2=(x_2-x_0,y_2-y_0)$，计算叉积：

$(p_1-p_0)\times (p_2-p_0)=(x_1-x_0)(y_2-y_0)-(x_2-x_0)(y_1-y_0)$

如果叉积为正，那么 $\vec{p_0p_1}$ 位于 $\vec{p_0p_2}$ 的顺时针方向；反之亦然。

确定连续线段是向左转还是向右转

利用叉积可以避免计算角度问题。方法如下：对于两条连续线段 $\vec{p_0p_1}$ 和 $\vec{p_0p_2}$ ，计算叉积 $(p_2-p_0)\times (p_1-p_0)$ ，若结果为正，则 $\vec{p_0p_2}$ 在 $\vec{p_0p_1}$ 的顺时针方向，即在 $p_1$ 处右转；反之亦然；若叉积为0，意味着 $p_0,p_1,p_2$ 三者共线。

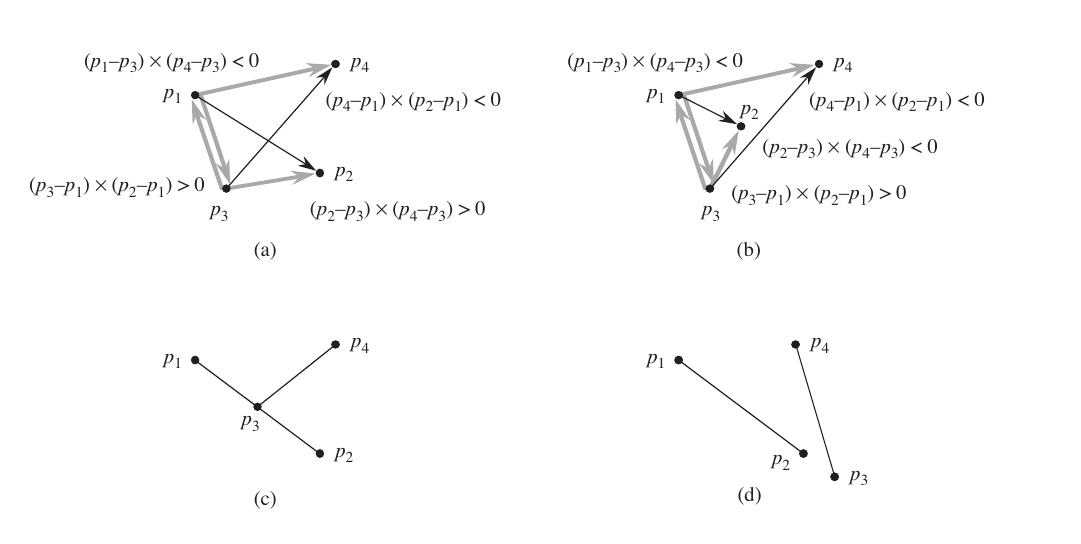
判定两条线段是否相交

需要检查每条线段是否跨越了包含另一条线段是直线。

伪代码如下

#include<stdio.h>
#include<stdlib.h>

struct point{ 
    int x; 
    int y;
    point(){}
    point(int _x,int _y):x(_x),y(_y){}
};

// 向量积计算线段的方向 pi 为相对原点
int direction(point p0,point p1,point p2){
    return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
}

int min(int a,int b){ return a<b?a:b; }
int max(int a,int b){ return a>b?a:b; }

// 判定一个和线段成直线所共线的点是否位于这条线段上
bool on_segment(point p0,point p1,point p2){
   if((min(p0.x,p1.x)<=p2.x<=max(p0.x,p1.x))
      &&(min(p0.y,p1.y)<=p2.y<=max(p0.y,p1.y))) return true;
   return false;
}

// 判定线段是否相交
bool segment_intersect(point p1,point p2,point p3,point p4){
    int d1=direction(p1,p2,p4);
    int d2=direction(p1,p2,p3);
    int d3=direction(p3,p4,p1);
    int d4=direction(p3,p4,p2);
    printf("d1:%d\td2:%d\td3:%d\td4:%d\n",d1,d2,d3,d4);
    if(((d1<0&&d2>0)||(d1>0&&d2<0)) && ((d3<0&&d4>0)||(d3>0&&d4<0))) return true;
    else if(d1==0&&on_segment(p1,p2,p4))return true;
    else if(d2==0&&on_segment(p1,p2,p3))return true;
    else if(d3==0&&on_segment(p3,p4,p1))return true;
    else if(d4==0&&on_segment(p3,p4,p2))return true;
    return false;
}

int main(){
    point p1(1,1),p2(4,4);
    point p3(3,3),p4(4,0);
    if(segment_intersect(p1,p2,p3,p4))
        printf("线段相交...\n");
    return 0;
}