数据结构-AVL树

AVL树是最早被发明的自平衡二叉查找树。其查找、插入和删除在平均和最坏情况下的时间复杂度都是 O(log⁡n)O(\log n)。AVL树由G. M. Adelson-Velsky和Evgenii Landis发明，AVL树的名称取自他们名字中的字母。

AVL树

在讨论AVL树之前先来看一下这张表

方法 最坏情况 平均情况
查找插入删除查找插入删除
有序数组 lognnnlognnn
有序链表 nnnnnn
跳表 nnnlognlognlogn
哈希表 nnn111
BST nnnlognlognlogn
AVL树 lognlognlognlognlognlogn
红黑树 lognlognlognlognlognlogn

在最坏情况下二叉查找树的复杂度为 O(n)O(n)，这种情况下BST出现严重“畸形”，或者退化成单链表。

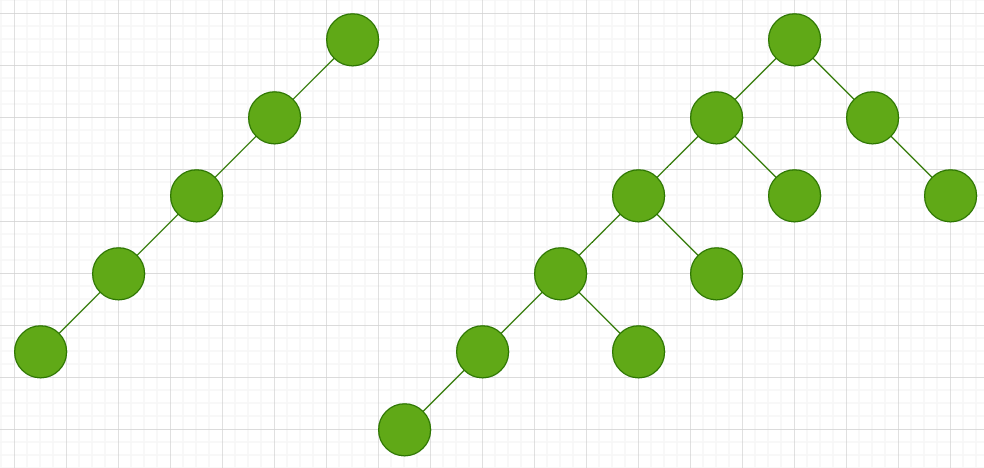
这些情况确实存在，那么如何保证不会出现“一边倒”情况呢？这时AVL树就该登场了。

首先来回顾之前的文章，了解到二叉查找树的性质3：

一棵二叉树有nn个元素，n>0n>0，它的高度最大为nn，最小高度为⌈log2(n+1)⌉\lceil log_2(n+1) \rceil。

AVL树要做的就是将 高度最大为nn 的情况尽可能的转化为 最小高度为⌈log2(n+1)⌉\lceil log_2(n+1) \rceil 。

AVL树也是二叉查找树！！！

特征

  • 一棵n个元素的AVL树高度为O(log⁡n)O(\log n)
  • 对一棵n个元素的AVL树，在O(Height)=O(log⁡n)O(Height)=O(\log n) 时间内可以实现查找操作
  • 对一棵n个元素的AVL树插入和删除，时间复杂度为O(log⁡n)O(\log n)

平衡因子bf

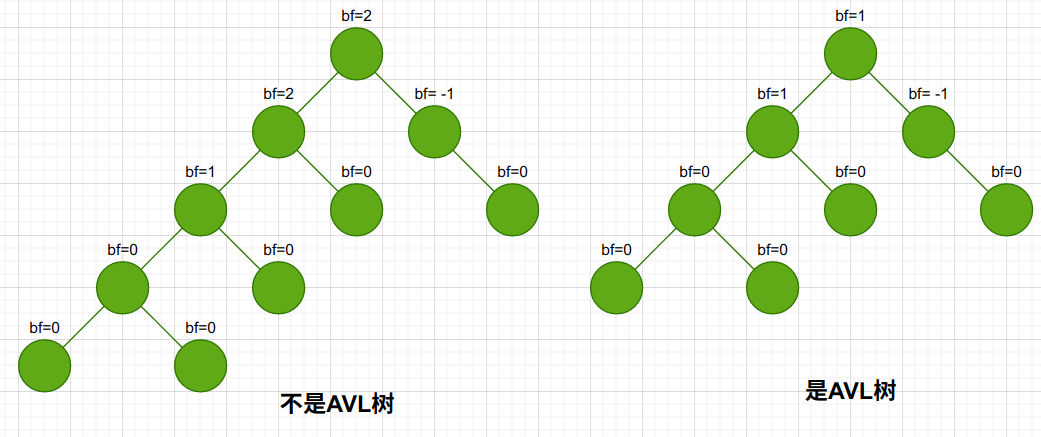
AVL树是通过平衡因子来调整二叉查找树结构使其平衡,且AVL树的平衡因子只能是 1、-1、0，否则该树不是AVL树
节点xx的平衡因子bf(x)bf(x)=xx的左子树高度-xx的右子树高度
由于平衡因子bf的限定，使得AVL树变成严格平衡二叉查找树

AVL树的旋转

造成二叉查找树的不平衡来自于插入和删除操作，在插入或删除一个节点时有几种不平衡状态，分别为“左左/LL”、“左右/LR”、“右右/RR”、“右左/RL”。AVL树要做的，就是处理这些不平衡结构。

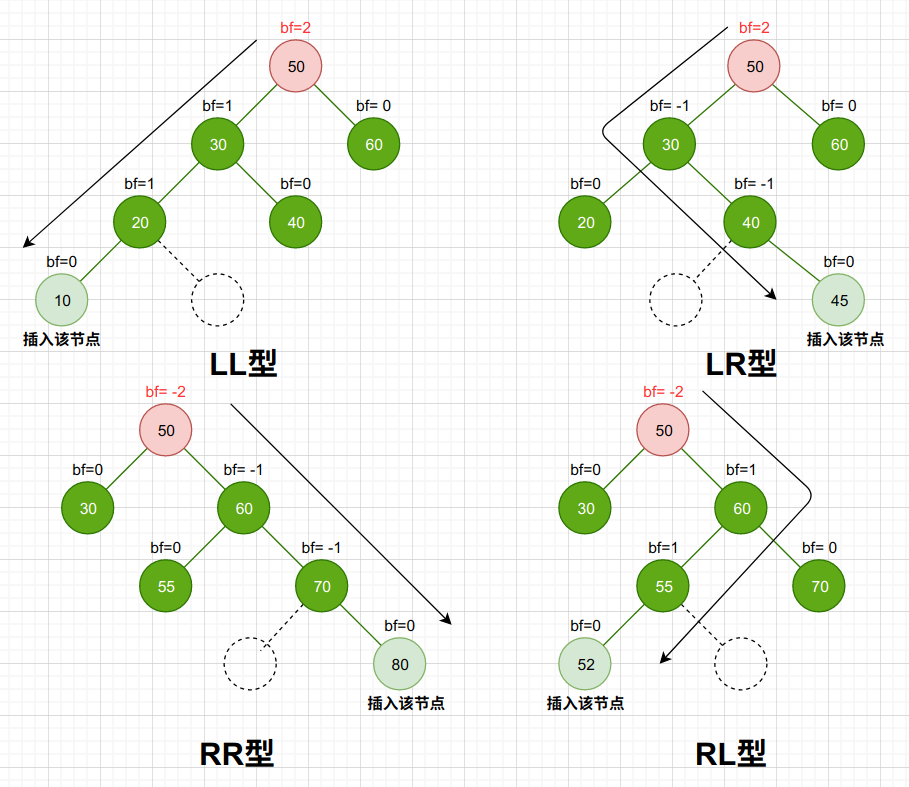
插入或删除一个节点后，导致根节点的 平衡因子=左子树的高度-右子树的高度=2，结果AVL树失去了平衡

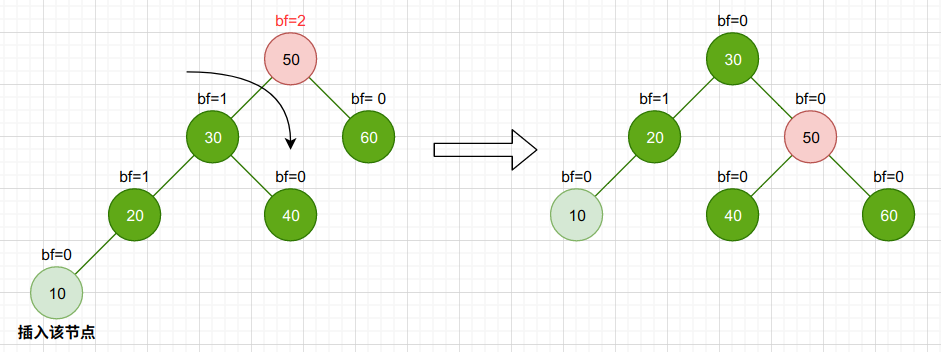
LL

旋转过程：
将平衡因子=2的根节点X的左节点L作为旋转后的根节点，同时将L的右孩子调整为X的左孩子。
最后更新各个节点的bf

RR

旋转过程：
将平衡因子=2的根节点X的右节点R作为旋转后的根节点，同时将R的左孩子调整为X的右孩子。
最后更新各个节点的bf

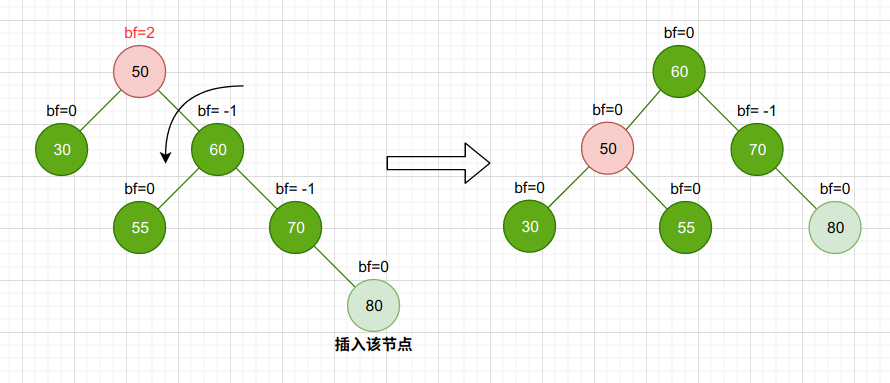
LR

LR型旋转需要两次旋转，即先左旋(RR)后右旋(LL)
首先围绕不平衡根节点bf=2的左孩子进行左旋，再围绕根节点进行右旋

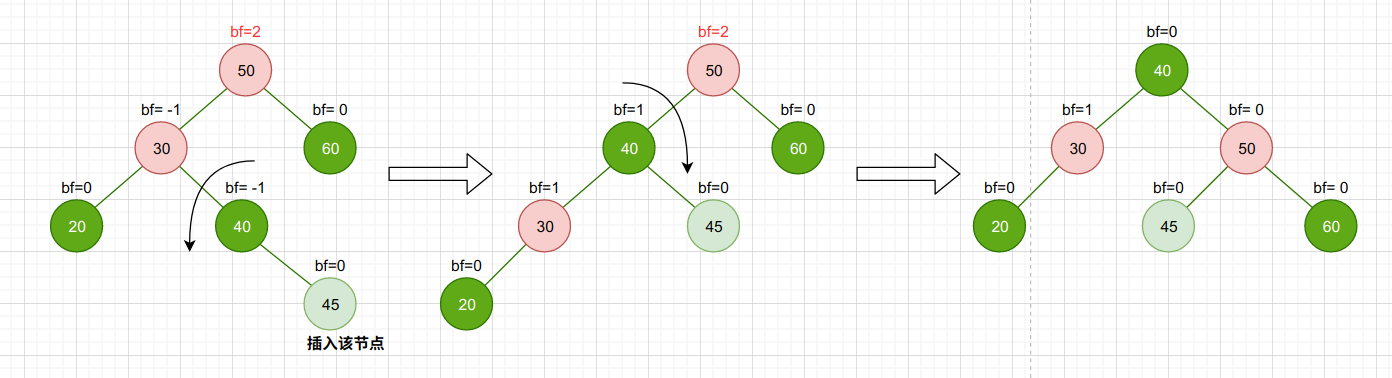
RL

RL型旋转也需要两次旋转，即先右旋(LL)后左旋(RR)
首先围绕不平衡根节点bf=2的右孩子进行右旋，再围绕根节点进行左旋

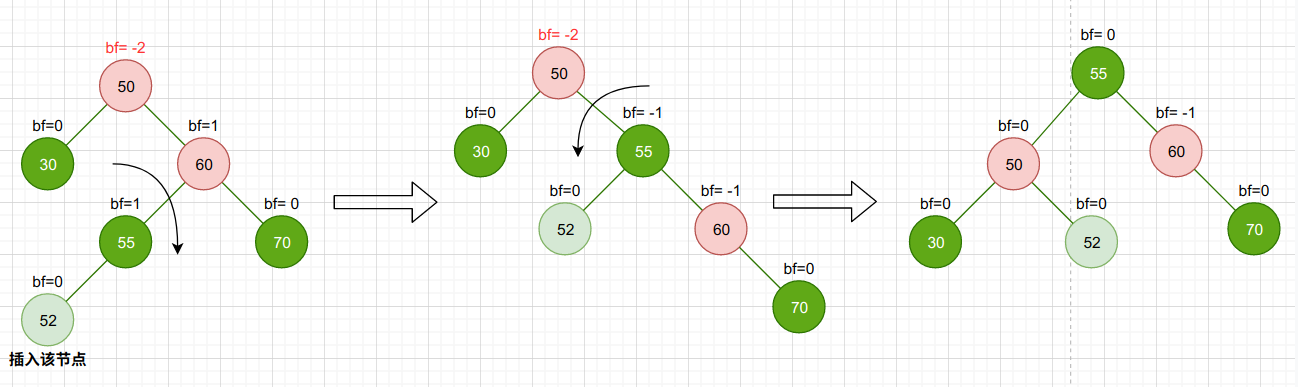
C++代码

首先定义一个节点结构体

1
2
3
4
5
6
7
8
9
template<class T>
struct AVLNodeEntry{
    int key;
    T data;
    int height;
    AVLNodeEntry *parent;
    AVLNodeEntry *left_nodes;
    AVLNodeEntry *right_nodes;
};

AVL树模板类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
template<class T>
class AVLTree {
private:
    AVLNodeEntry<T>* m_NodeRoot;
    int m_binaryTree_length;
    int m_m_binaryTree_maxKey;
    int m_m_binaryTree_minKey;
    bool m_isClear;
public:
    AVLTree();
    AVLTree(int  k,const T& v);
    ~AVLTree();

    int Height(AVLNodeEntry<T>* pNode);
    void Insert(AVLNodeEntry<T>* & pNode,AVLNodeEntry<T>* pNodeParent,int key,const T& value);
    bool Remove(AVLNodeEntry<T>* pNode,int key);
    void Delete(AVLNodeEntry<T>* & pNode,int key);
    AVLNodeEntry<T>* & GetRootNoder();
    
    AVLNodeEntry<T>* Search(AVLNodeEntry<T>* pNode,int key);
    AVLNodeEntry<T>* GetMaxNode();
    AVLNodeEntry<T>* GetMinNode();
    AVLNodeEntry<T>* predecessor(AVLNodeEntry<T>* cur_node);
    AVLNodeEntry<T>* successor(AVLNodeEntry<T>* cur_node);

    static AVLNodeEntry<T>* CreateElementBy(int  key,const T& value,AVLNodeEntry<T>* pParent= nullptr);
   
    void ClearAll(AVLNodeEntry<T>* & pNode);
    void PreOrder(AVLNodeEntry<T>* pRootNode);
    void InOrder(AVLNodeEntry<T>* pRootNode);
    void PostOrder(AVLNodeEntry<T>* pRootNode);
    void LevelOrder(AVLNodeEntry<T>* pRootNode);

    // 计算节点的高度
    void CalcHeight(AVLNodeEntry<T>* pNode){
        if(!pNode)return;
        pNode->height=std::max(Height(pNode->left_nodes),Height(pNode->right_nodes))+1;
    }

    AVLNodeEntry<T>* LLRotation(AVLNodeEntry<T>* &pRootNode);
    AVLNodeEntry<T>* RRRotation(AVLNodeEntry<T>* &pRootNode);
    AVLNodeEntry<T>* LRRotation(AVLNodeEntry<T>* &pRootNode);
    AVLNodeEntry<T>* RLRotation(AVLNodeEntry<T>* &pRootNode);
};

旋转

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
template<class T>
AVLNodeEntry<T>* AVLTree<T>::LLRotation(AVLNodeEntry<T>* &pRootNode){
    if(!pRootNode)return pRootNode;
    AVLNodeEntry<T>*  leftChild=pRootNode->left_nodes;
    pRootNode->left_nodes=leftChild->right_nodes;
    if(leftChild->right_nodes!=nullptr){
        leftChild->right_nodes->parent=pRootNode;
    }
    leftChild->right_nodes=pRootNode;
    
    leftChild->parent=pRootNode->parent;
    pRootNode->parent=leftChild;

    CalcHeight(pRootNode);
    CalcHeight(leftChild);

    pRootNode=leftChild;
    if(pRootNode->parent==nullptr)
        this->m_NodeRoot=pRootNode;
    return leftChild;
}

template<class T>
AVLNodeEntry<T>* AVLTree<T>::RRRotation(AVLNodeEntry<T>* &pRootNode){
    if(!pRootNode)return pRootNode;
    AVLNodeEntry<T>*  rightChild=pRootNode->right_nodes;
    pRootNode->right_nodes=rightChild->left_nodes;
    if(rightChild->left_nodes!=nullptr){
        rightChild->left_nodes->parent=pRootNode;
    }
    rightChild->left_nodes=pRootNode;

    rightChild->parent=pRootNode->parent;
    pRootNode->parent=rightChild; 

    CalcHeight(pRootNode);
    CalcHeight(rightChild);

    pRootNode=rightChild;
    if(pRootNode->parent==nullptr)
        this->m_NodeRoot=pRootNode;
    return rightChild;
}

template<class T>
AVLNodeEntry<T>* AVLTree<T>::LRRotation(AVLNodeEntry<T>* &pRootNode){
    this->RRRotation(pRootNode->left_nodes);
    return this->LLRotation(pRootNode);
}

template<class T>
AVLNodeEntry<T>* AVLTree<T>::RLRotation(AVLNodeEntry<T>* &pRootNode){
    this->LLRotation(pRootNode->right_nodes);
    return this->RRRotation(pRootNode);
}

插入

插入一个新节点后，可能导致AVL树不平衡，因此需要判断平衡因子bf，若bf为2或-2说明需要进行旋转操作。不过只需要判断bf是否为2即可，这是由遍历的顺序决定的。
每次插入完成都需要更新节点的高度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

template<class T>
void AVLTree<T>::Insert(AVLNodeEntry<T>* & pNode,AVLNodeEntry<T>* pNodeParent,int key,const T& value) {
    if(pNode == nullptr){
        pNode=new AVLNodeEntry<T>;
        pNode->key=key;
        pNode->left_nodes= nullptr;
        pNode->right_nodes= nullptr;
        pNode->data=value;
        pNode->parent=pNodeParent;
        pNode->height=1;
        return;
    }
    // 遍历左子树
    else if(key < pNode->key){
        Insert(pNode->left_nodes,pNode,key,value);
        // 插入完成后检查是否平衡了
        // 若平衡因子为2表示不平衡
        // 只需要判断左右两边树的高度之差
        if(Height(pNode->left_nodes)-Height(pNode->right_nodes)==2){
            if(key < pNode->left_nodes->key){
                this->LLRotation(pNode);
            }else{
                this->LRRotation(pNode);
            }
        }

    }// 否则右子树
    else if(key > pNode->key){
        Insert(pNode->right_nodes,pNode,key,value);
        // 插入完成后检查是否平衡了
        if(Height(pNode->right_nodes)-Height(pNode->left_nodes)==2){
            if(key > pNode->right_nodes->key){
                this->RRRotation(pNode);
            }else{
                this->RLRotation(pNode);
            }
        }
    }//如果已经存在了
    else{
        //cout<<"Already exist!"<<endl;
        return;
    }
    // 插入完成后更新高度!
    // 从 0 开始计数，因此需要加1
    CalcHeight(pNode); // +1表示包括当前根节点
}

删除

删除操作类似二叉查找树的删除操作，同样需要找到一个前驱/后继节点。
不过此处删除操作是在一个递归函数中进行的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
template<class T>
void AVLTree<T>::Delete(AVLNodeEntry<T>* & pNode,int key) {
    if(!pNode)return;
    if (key < pNode->key){
        // 在左子树中删除一个节点
        Delete(pNode->left_nodes,key);
        // 删除后重新平衡
        if(Height(pNode->right_nodes)-Height(pNode->left_nodes)==2){ 
            if(Height(pNode->right_nodes->left_nodes)>=Height(pNode->right_nodes->right_nodes)){
                RLRotation(pNode);
            }else{
                RRRotation(pNode);
            }                
        }
    }else if (key > pNode->key){
        // 在右子树中删除一个节点
        Delete(pNode->right_nodes,key);
        if (Height(pNode->left_nodes)-Height(pNode->right_nodes)==2){
            if(Height(pNode->left_nodes->left_nodes)>=Height(pNode->left_nodes->right_nodes)){
                LLRotation(pNode);
            }else{
                LRRotation(pNode);
            }
        }
    }else{
        // 左右子树都存在
        if (pNode->left_nodes&&pNode->right_nodes){
            // 找到一个后继节点 
            AVLNodeEntry<T>* successor=this->successor(pNode);
            pNode->key=successor->key;
            pNode->data=successor->data;
            // 删除那个后继节点
            Delete(pNode->right_nodes,successor->key);
            // 然后再次重新平衡
            if(Height(pNode->left_nodes)-Height(pNode->right_nodes)==2){
                if(Height(pNode->left_nodes->left_nodes)>=Height(pNode->left_nodes->right_nodes)){
                    LLRotation(pNode);
                }else{
                    LRRotation(pNode);
                }
            }
        }else{
            // 删除只有一个子树和叶子情况
            auto pDeleteNode=pNode;
             // 保存其子节点，无论是否为空
            AVLNodeEntry<T>* childNode=nullptr;
            if(pDeleteNode->left_nodes!=nullptr){
                childNode=pDeleteNode->left_nodes;
            }else if(pDeleteNode->right_nodes!=nullptr){
                childNode=pDeleteNode->right_nodes;
            }
            // 如果存在子节点（不是叶子），那么修改其指向父节点
            if(childNode!=nullptr){
                childNode->parent=pDeleteNode->parent;
            }
            // 删除的是根节点
            if(pDeleteNode->parent==nullptr){
                this->m_NodeRoot=childNode;
            }else if(pDeleteNode->parent->left_nodes==pDeleteNode){
                // 修改待删除节点的父节点指向待删除节点的子节点
                pDeleteNode->parent->left_nodes=childNode;
            }else if (pDeleteNode->parent->right_nodes==pDeleteNode){
                pDeleteNode->parent->right_nodes=childNode;
            }
            delete pDeleteNode;
            pDeleteNode=nullptr;
        }
    }
    // 跟新节点高度
    if(pNode){
        CalcHeight(pNode);
    }
}

源码： https://josephxrays.coding.net/p/avlTree_c/git