对于大部分人来说掌握词法分析和语法分析前端知识还是很有必要的，而且适用的场景有很多，比如在实现一些命令解析器或者造一个json解析库还是非常有用的

语法分析

上下文无关文法

组成L：

• 终结符号集合 $T$，最基本的词法单元。比如 $+-*/()\ id$
• 非终结符号集合 $N$。比如 $stmt,expr$，换句话说就是还可以继续推导出其他的 非终结符号和终结符号
• 开始符号 $S$
• 产生式集合 $P$ 。产生式用 $\rightarrow$ 表示出对应的右边的串

一个普通的产生式写作 $A\rightarrow \alpha$

终结符只能出现在产生式的右边，非终结符则左边和右边都可以出现

终结符和非终结符统称为符号，符号一般用字母 A, B, X, Y, a, b 表示，符号串一般用小写字母 u, v 表示。产生式的形式为 A -> u ，其中 A 为非终结符， u 为一个符号串。

推导

将产生式看作重写规则，就可以从推导的角度精确地描述构造语法分析树的方法。从开始符号开始，每个重写步骤把一个 非终结符号 替换为它的 某个产生式的体。（谁最先被替换）

$E\Rightarrow -E$ 读作 E推导出 -E 。

• 在最左推导中，总是选择每个句型的 最左非终结符号，如果 $\alpha\Rightarrow\beta$ 是一个推导步骤，且被替换的是 $\alpha$ 中的最左非终结符号，写作 $\alpha\Rightarrow _{lm}\beta$ （把最左非终结符号替换为终结符号）
• 在最右推导中，总是选择每个句型的 最右非终结符号，如果 $\alpha\Rightarrow\beta$ 是一个推导步骤，且被替换的是 $\alpha$ 中的最右非终结符号，写作 $\alpha\Rightarrow _{rm}\beta$（把最右非终结符号替换为终结符号）

对月一个给定的文法 $E$

$E\rightarrow E+E|E*E|-E|(E)|\text{id}\\$

如果有一个表达式 $-(id+id)$，根据 最左推导 或者 最右推导可以得到以下两种不同的推导过程（替换的顺序不同）

1. 最左推导：$E\rightarrow -E$

$-(id+id)$的推导过程如下：

$E\Rightarrow -E$

$E\Rightarrow -(E)$

$E\Rightarrow -(E+E)$

$E\Rightarrow -(id+E)$

$E\Rightarrow -(id+id)$

对应的语法分析树如下

 E
/  \
  -   E
  / | \
 (  E  )
  / | \
 E  +  E
 |	   |
 id	   id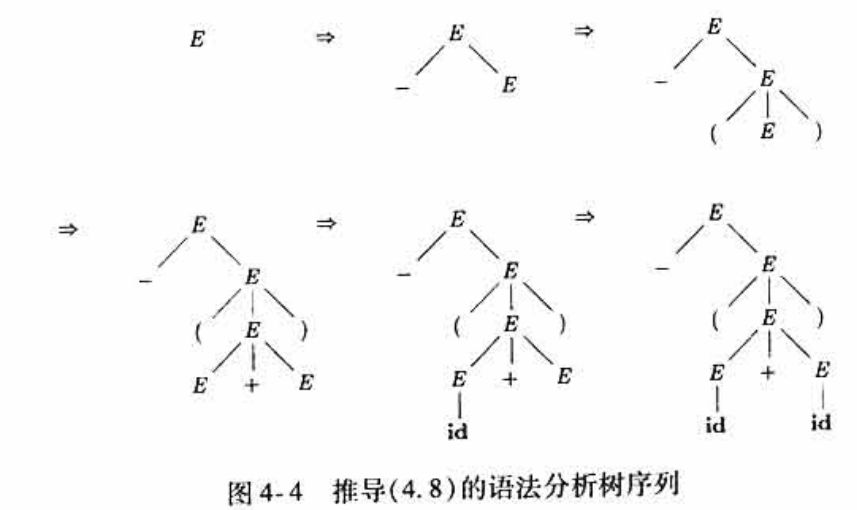

2. 最右推导：$E\rightarrow -E$

$E\Rightarrow -E$

$E\Rightarrow -(E)$

$E\Rightarrow -(E+E)$

$E\Rightarrow -(E+id)$

$E\Rightarrow -(id+id)$

二义性

如果一个文法可以为某个句子生成多棵语法分析树，那么就是二义性的。即： 二义性文法就是对同一个文法有多个最左推导或多个最右推导的文法。

对于算术表达式文法 $id+id*id$ 具有两种最左推导，消除二义性的一个方法是根据 优先级 在推导的过程中处理

最左/右推导

S -> S S + | S S * | a
S =lm=> SS* => SS+S* => aS+S* => aa+S* => aa+a*
S =rm=> SS* => Sa* => SS+a* => Sa+a* => aa+a*

S -> S + S | S S | (S) | S*
S =lm=> SS => S*S => (S)*S => (S+S)*S => (a+S)*S => (a+a)*S => (a+a)*a
S =rm=> SS => Sa => S*a => (S)*a => (S+S)*a => (S+a)*a => (a+a)*a

上下文无关文法和正则表达式

文法比正则表达式表达能力更强，换句话说每个正则语言都是一个上下文无关文法，反之不成立。

词法分析和语法分析

为什么使用正则表达式来定义一个语言的词法语法？

• 将一个语言的语法结构分为 词法 和 非词法 两部分可以方便的将编译期前端模块化
• 一个语言的词法规则通常很简单，我们不需要使用像文法这样的功能强大的表示方法来描述这些规则
• 和文法相比，正则表达式通常提供更加简洁且易于理解的表示 词法单元 的方法
• 效率高

正则表达式最适合描述诸如 标识符，常量，关键字，空白 这样的语言构造的结构。

文法最适合描述 嵌套结构，比如 对称的括号对，匹配的begin-end，相互对应的 if-then-else，这些无法用正则表达式来描述。

消除二义性

这里以消除 悬空-else 为例来消除文法中的二义性，比如下面的文法就是二义性的

语法分析树如下：

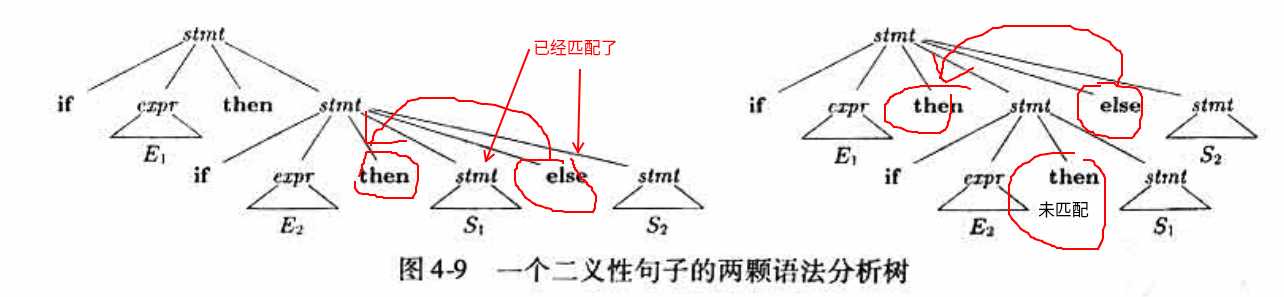
对应的代码层次结构为

>if expr 
>then 
   if expr 
   then stmt
   else stmt // 产生 歧义

>if expr 
>then
   	if expr 
   	then stmt
>else stmt	// 产生 歧义

注意第二个代码的解析层次结构中最后一个 else stmt 也是可以放在内部的 if 后面的。所以在语义分析时这两语法分析树具有二义性！

这里总是会选择第一颗语法分析树，通用的规则是： 每个else和最近的尚未匹配的then匹配。

我们我可以将悬空-else文法改写成如下无二义性的文法，基本思想是在一个then和一个else之间出现的语句必须是 已经匹配的（意思就是不包含if-then-else的语句 或者 非条件语句），也就是说，中间的语句不能以一个尚未匹配（开放）的then结尾，这就限制了else必须和最近的尚未匹配的then匹配

比如上面的第一颗语法分析树中，else和左边最近的尚未匹配的then中间有一个 非条件语句，因此应该选择第一颗语法分析树；对于第二颗语法分析树，else和左边的then虽然匹配，但是在 then-else中间还有一个 if-then-ese语句 导致那个then还没有某个else和他进行匹配。

左递归的消除

如果一个文法中有一个非终结符号 A 使得对某个串 $\alpha$ 存在一个推导 $A\Rightarrow A\alpha$，那么这个文法就是 左递归 的，自顶向下语法分析不能处理左递归的方法，因此需要一个转换方法来消除左递归。

立即左递归 可以使用下面的技术消除，该技术可以处理任意的 A 产生式。首先将A的全部产生式分组如下

$A\rightarrow A\alpha_1|A\alpha_2|...|A\alpha_m|\beta_1|\beta_2|...|\beta_m$

其中 $\beta_i$ 都不以 $A$ 开头（除此之外也就是说，既可以是其他的 终结符号 也可以是 非终结符号）。然后，将这些 A 产生式替换为：

$A\rightarrow \beta_1A'|\beta_2A'|...|\beta_mA'\\ A'\rightarrow \alpha_1A'|\alpha_2A'|...|\alpha_mA'|\epsilon$

比如 $E\rightarrow E+T|T$ 左递归可以转换为 $E\rightarrow TE'$ 和 $E'\rightarrow +TE'|\epsilon$。

但是上面的替换式子无法消除那些因为两步或多步推导而产生的左递归。比如

$S\rightarrow Aa|b\\ A\rightarrow Ac|Sd|\epsilon$

这里由于 $S\Rightarrow Aa \Rightarrow Sda$ 是有两步推导而得到的，但这不是立即左递归！因此无法用上面的公式消除。

下面的算法系统地消除了文法中的左递归。如果文法中不存在 环 （即形如 $A\Rightarrow A$ 的推导） 或 $\epsilon$ 产生式（即形如 $A\rightarrow\epsilon$ 的产生式），这样的话就能保证能够消除左递归。

算法：消除左递归

输入： 没有环或 $\epsilon$ 产生式的文法 $G$

输出： 一个等价的的无左递归的文法

注意，得到的非左递归文法中可能具有 $\epsilon$ 产生式

这个算法的内层循环负责将将当前的产生式 $A_i$ 中的非终结符号 $A_j$ 替换为根据 “之前” 得到的所有产生式中的串（已知），这样就可以让当前这个产生式 $A_i$ 变为 立即左递归，然后由外层循环 消除每个产生式的立即左递归。

将非终结符号按照某个顺序排序
for(int i=1; i<=n; i++){
    for(int j=1; j<=i-1; j++){
        将形如A[i]->A[j]r中的A[j]替换为A[j]所对应的所有属于A[j]的产生式
    }
    消除A[i]产生式的立即左递归
}

例子1

$A_1=S\rightarrow A\ a|b\\ A_2=A\rightarrow A\ c|S\ d|\epsilon$

首先将非终结符号排序为$S,A$。由于在 $S$ 产生式之间没有立即左递归，因此在 $i=1$ 的外层循环中不进行任何处理。

当 $i=2$ 时，将每个形如 $A\rightarrow Sd$ 替换，也就是替换 $A\rightarrow Sd$ 中的 $S$（A原来的串保持不变） ，于是得到如下的 $A$ 产生式：$A\rightarrow A\ c|A\ a\ d|b\ d|\epsilon$。这样就得到了以i个 立即左递归。然后根据之前的替换公式再将这个立即左递归消除即可：（注意这个文法中由于含有 $A\rightarrow \epsilon$ 产生式，因此得到的结果文法不一定正确！）

• 先将立即左递归分组为 $A\rightarrow A\ c|A\ a\ d|b\ d|\epsilon$
• 再将 $A$ 产生式替换，最终得到的等价的非左递归文法 $G$

$S\rightarrow A\ a|b \\ A\rightarrow b\ d A' |A'\\ A'\rightarrow c\ A'|a\ d\ A'|\epsilon$

例子2

消除立即左递归

rexpr -> rexpr + rterm | rterm
rterm -> rterm rfactor | rfactor
rfactor -> rfactor * | rprimary
rprimary -> a | b

   rexpr -> rterm A
       A -> + rterm A | ε
   rterm -> rfactor B
       B -> rfactor B | ε
 rfactor -> rprimary C
       C -> * C | ε
rprimary -> a | b

提取左公因子

提取左公因子是一个文法转换，他可以适用于预测分析技术或自顶向下的分析技术。当不知道应该从两个A产生式中如何选择时，可以通过改写产生式来推后这个决定，等我们读入了足够多的输入再做正确的选择。

对于 $A\rightarrow \alpha\beta_1|\alpha\beta_2$ 可以将 $A$ 展开为 $\alpha A'$，从而延后这个决定。再读入了从 $\alpha$ 推导得到的输入前缀后，在决定将 $A'$ 展开为 $\beta_1$ 还是 $\beta_2$

算法：对一个文法提取左公因子

输入：文法G

输出：一个等价的提取了左公因子的文法

方法：对每个非终结符号A，找出他的两个或多个选项之间的 最长公共前缀 $\alpha$ 。如果 $\alpha\ne \epsilon$ ，即存在一个 非平凡的公共前缀，那么将所有 A 产生式 $A\rightarrow \alpha\beta_1|\alpha\beta_2|...|\alpha\beta_n|\gamma$ 替换为

$A\rightarrow \alpha A'|\gamma\\ A'\rightarrow \beta_1|\beta_2|...|\beta_n$

例子

自顶向下的语法分析

递归下降的语法分析

通用的递归下降分析技术可能需要回溯，然而实际上很少需要回溯，一般的做法是采用 动态规划 基于表格的方法

注意，一个 左递归 的文法会使他的 递归下降语法分析 进入一个 无限循环，这是因为当我们试图展开一个 非终结符号A 时，在没有读入任何输入符号（没有 消费 输入符号）的情况下就再次展开了，导致陷入无限递归。

FIRST首符号集合 和 FOLLOW后继符号集合

FIRST和FOLLOW可以让我们根据下一个输入符号来选择应用哪个产生式。

$\text{FIRST}(\alpha)$ ：可从任意的文法符号串 $\alpha$ 推导得到串的 首字符 的 集合。比如 $A\Rightarrow c\gamma$ ，因此 $c$ 在 $\text{FIRST}(A)$ 中。$\epsilon $也可以在 FIRST中

在预测分析中使用 FIRST ：比如有一个产生式 $A\rightarrow \alpha|\beta $ （注意，这里是希腊字母，$\alpha,\beta$ 表示文法符号串），其中 $\text{FIRST}(\alpha)$ 和 $\text{FIRST}(\beta)$ 是不相交的集合。那么只需要查看下一个输入符号 $a$ （小写英文字母），就可以在这两个 $A$ 产生式中进行选择。

对于非终结符号 $A$ ，$\text{FOLLOW}(A)$ ：可能在某些句型中紧跟在 $A$ 右边的 终结符号 的集合。比如 $S\Rightarrow \alpha Aa\beta$ 的推导，其中 $a$ 就在 $\text{FOLLOW}(A)$ 中。注意，在这个推导的某个阶段， $A$ 和 $a$ 之间可能存在一些文法符号，这样的话，这些符号会推导得到 $\epsilon$ 并导致 a 消失。另外，如何 $A$ 是某些句型的最右边符号，那么我们可以假设存在一个 结束标记$ 符号也在 FLLOW(A) 中。

FIRST集合

对于一个产生式 $X\rightarrow Y_1 Y_2Y_3...Y_n$ ，

• 如果 $X$ 是一个 终结符号，则 $\text{FIRST}(X)=X$
• 如果 $X$ 是一个 非终结符号， 且 $X\rightarrow Y_1 Y_2Y_3...Y_n$ 是一个产生式。对于某个 $i,a$ 在 $\text{FIRSTY}(Y_i)$ 中且 $\epsilon$ 在 $Y_1,Y_2,...,Y_{i-1}$（$Y_1,Y_2,...Y_{i-1}\Rightarrow \epsilon$） ，则将 $a$ 加入到 $\text{FIRST}(X)$中。（为什么需要 $\epsilon$ 位于所有的子产生式中？因为只有 $\epsilon$ 位于每一个子产生式中时，才会有一个可以分配出去的首字符，这样才可以将该首字符传递给另外一个大的产生式。比如 $C \rightarrow b|\epsilon$，有一个 $\epsilon$ ，因此 $A$ 在推导的时候可以推导/展开出 $C$ 的 下一个字符 a ！！！，或者换句话说，因为有 $\epsilon $ 所以才会有机会得到子产生式的 后面一个字符）
• 如果 $X\rightarrow \epsilon$ 是一个产生式，则将 $\epsilon$ 加入到 $FIRST(X)$ 中

C -> b|e

A -> Ca|e

​ -> ba|a|e

FIRST© = {b ,e }

FIRST(A) = {a, b, e}

FOLLOW集合

所有 非终结符号 的FOLLOW集合

• 将 $ 加入到 FOLLOW(S) 中，S为开始符号，$ 为结束标记

• 若存在一个产生式 $A\rightarrow \alpha B \beta$，则对于 $FIRST(\beta)$ 中除了 $\epsilon$ 之外的 所有符号 都在 $FOLLOW(B)$ 中。

• 若存在一个产生式 $A\rightarrow \alpha B$ ，或存在一个产生式 $A\rightarrow \alpha B\beta$ 且 $FIRST(\beta)$ 包含 $\epsilon$ ，则 $FOLLOW(A)$ 中的所有符号都在 $FOLLOW(B)$中，即 $\text{FOLLOW}(A)\sub \text{FOLLOW}(B)$。

  为什么？这是因为如果 $\epsilon\in\text{FIRST}(\beta)$ ，说明 $\beta$ 这个符号 可以省略 （因为空字符 $\epsilon$ 可以跳过，直接得到下一个符号，假设为 $x$），这样在推导的过程中可以直接推导下一个符号 $x$！那么为什么又说 FOLLOW(A) 中的所有符号都在FOLLOW(B) 中呢？这是因为 对于产生式 $A\rightarrow \alpha B$ 是从左到右推导的，换句话说就是在字符串匹配时，用 $\alpha B$ 来替换掉左部的非终结符号 $A$ ，但是对于非终结符号 $A$ 它可能也会保留一些状态（也就是FIRST和FOLLOW集合），因此在替换为产生式体的符号时，需要 保留/继承 左部原来的 FOLLOW(A) 集合，也就是将 FOLLOW(A) 加入到 当前的非终结符号的 FOLLOW(B) 集合内。

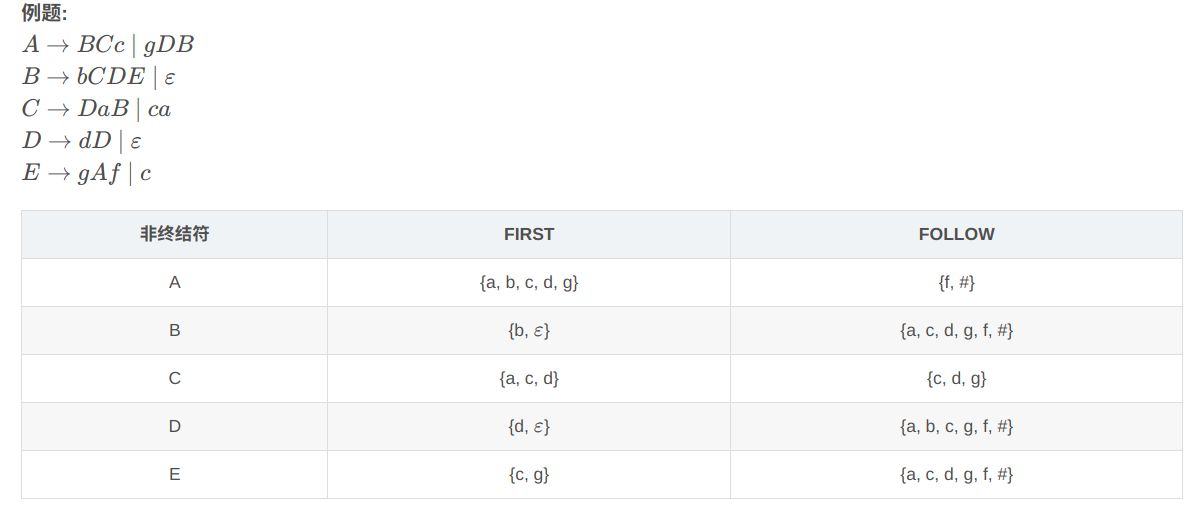
如求A的，产生式：

S→ABc

A→a|ε

但只有 S→ABc 有用。跟随在A后年的终结符号是 FIRST（B）=｛b，ε｝，当FIRST（B）的元素为ε时，跟随在A后的符号就是c，所以 Follow（A）=｛b，c｝ 同理Follow（B）=｛c｝

总之就是：

若一个符号串 u = X1 X2 … Xn ，则 First(u) 的计算步骤如下：

（1） 置 i = 1 ；

（2） 若 i == n + 1，则将 ε 加入 First(u) ，终止计算；

（3） 若 Xi 是终结符，则将 Xi 加入 First(u) ，终止计算；

（4） 若 Xi 是非终结符，则将 First(Xi) - ε 加入 First(u)，

​ 4.1 若 First(Xi) 不含 ε ，则终止计算；

​ 4.2 若 First(Xi) 中含有 ε ，则置 i = i + 1 ，转到（2）。

一个语法中所有非终结符的 follow set 的计算步骤如下：

（1） 将 $ 加入到 Follow(S) 中， S 为起始符号， $ 为结束符 EOF ；

（2） 对每条形如 A -> u B v 的产生式，将 First(v) - ε 加入到 Follow(B) ；

（3） 对每条形如 A -> u B 的产生式，或 A -> u B v 的产生式（其中 First(v) 含 ε ），将 Follow(A) 加入到 Follow(B) 。

求FOLLOW例题

S→ABc
A→a|ε
B→b|ε

First集合求法:
能由 非终结符号 推出的所有的 开头符号或可能的ε，但要求这个开头符号是终结符号。如此题A可以推导出a和ε，所以FIRST（A）=｛a，ε｝；同理 FIRST（B）={b,ε};S可以推导出aBc，还可以推导出bc，还可以推导出c，所以FIRST(S）=｛a，b，c｝
Follow集合的求法:
紧跟随其后面的终结符号或＃。但文法的识别符号包含＃，在求的时候还要考虑到ε。 具体做法是把所有包含你要求的符号的产生式都找出来，再看哪个有用。 Follow（S）=｛＃｝
如求A的，产生式：S→ABc , A→a|ε ，但只有S→ABc 有用。跟随在A后面的终结符号是FIRST（B）=｛b，ε｝，当FIRST（B）的元素为ε时，跟随在A后的符号就是c，将 FOLLOW© 加入到 FOLLOW(A)，所以 Follow（A）=｛b，c｝ 同理Follow（B）=｛c｝

推荐博客文章：

• https://blog.csdn.net/jack_wong2010/article/details/9074951
• https://blog.csdn.net/liujian20150808/article/details/72998039

FIRST集求法

First集合最终是对产生式右部的字符串而言的，但其关键是求出非终结符的First集合，由于终结符的First集合就是它自己，所以求出非终结符的First集合后，就可很直观地得到每个字符串的First集合。

• 接收取：对形如U－>a…的产生式（其中a是终结符），把a收入到First(U)中
• 反复传送：对形入U－>P…的产生式（其中P是非终结符），应把First§中的全部内容传送到First(U)中【意思就是只需要把第一个非终结符的First集传过去】。

FOLLOW集的求法

Follow集合是针对非终结符而言的，Follow(U)所表达的是句型中非终结符U所有可能的后随终结符号的集合，特别地，“#”是识别符号的后随符。注意Follow集合是从 开始符号S 开始推导。

• 直接收取：注意产生式右部的每一个形如“…Ua…”的组合，把a直接收入到Follow(U)中。因a是紧跟在U后的终结符。
• 直接收取：对形如“…UP…”(P是非终结符)的组合，把 First§ 直接收入到 Follow(U) 中【在这里，如果First（P）中有空字符 $\epsilon$，那么就要把P的左部（即 …U…PS…）（假设是S，S也可能是非终结和终结符号）的 Follow（S） 送入到 Follow（U） 中。还有就是Follow集中是没有空字符的】。
• 直接收取：若S－>…U，即以U结尾，则 #∈Follow(U)
• *反复传送：对形如U－>…P的产生式（其中P是非终结符），应把Follow(U)中的全部内容传送到Follow§中。

图片来自上述博客

为什么要引入FOLLOW集的概念

考虑文法G[S]:
S→aA
S→d
A→bAS
A→ε
求得各终结符和符号串的FIRST集合如下:
FIRST(S) = {a,d}
FIRST(A) = {b,ε}
FIRST(aA) = {a}
FIRST(d) = {d}
FIRST(bAS) = {b}
FIRST(ε) = {ε}

若输入串 W=abd，则试图推导出abd串的推导过程为S⇒aA⇒abAS⇒abS⇒abd

从以上推导过程中可以看到，在第2步到第3步的推导中，即abAS⇒abS 时，因为当前面临的输入符号为d，但是最左非终结符A的产生式右部的开始符号集都不包含d，但有ε，因此对于d的匹配自然认为只能依赖于在可能的推导过程中A的后面的符号，所以这时候选用产生式A→ε 向下推导。而当前A后面的符号为S, S产生式右部的开始符号集包含了d，所以例子中可用S→d推导得到匹配。

也可以这么理解 $\epsilon$ ：当前没有产生式可以推导出下一个输入符号d，但是我可以 尝试 跳过 $\epsilon$ 当前这个非终结符号A，由后面的非终结符号S去推导得到该符号 S->d，最终也能够够推导成功。

LL(1)

LL(1)是一种自顶向下分析方法，也就是 从左到右扫描输入，产生最左推导，同时在每一步中只需要向前看一个输入符号来决定语法分析动作。

构造预测分析表/动作表M

• 输入：文法 G
• 输出：预测分析表 M

方法：对于文法 G的每一个产生式 $A\rightarrow \alpha$ ，进行如下处理

• 对于 $\text{FIRST}(\alpha)$ 中的 每一个 终结符号 $a$，将 $A\rightarrow \alpha$ 加入到 $M[A,a]$ 中
• 如果 $\epsilon\in \text{FIRST}(\alpha)$ ，那么对于 $\text{FOLLOW}(A)$ 中的 每一个 终结符号 $b$，将 $A\rightarrow \alpha$ 加入到 $M[a,b]$ 。如果 $\epsilon\in \text{FIRST}(\alpha)$ 且 $\$ \in \text{FOLLOW}(A)$ ，则将 $A\rightarrow \alpha$ 加入到 $M[A,\$]$。

动作表中的 $M[A, a]$ 保存了在解析过程中当栈顶为非终结。符 A 、读入的符号为 a 时所应采取的动作。

总之，表格中填入的是产生式 $A\rightarrow \alpha$，空条目表示预测分析错误

对语法中的每条产生式： A -> u ：

（1） 对 First(u) 中的所有终结符 a （不含 ε ），置 M[A, a] = “A -> u” ；

（2） 若 First(u) 含 ε ，则对 Follow(A) 中的所有符号 a （可含 $ ），置 M[A, a] = “A -> u” 。

例子

E   –>  T E'
E'  –>  + T E' | ε
T   –>  F T'
T'  –>  * F T' | ε
F   –> ( E ) | int

要解析的句子为： int + int * int

首先计算出所有非终结符的 first set 和 follow set ：

First(E)  = First(T) = First(F) = { ( int }
First(T') = { * ε}
First(E') = { + ε}

Follow(E) = Follow(E') { $ ) }
Follow(T) = Follow(T') = { + $ ) }
Follow(F) = { * + $ ) }

非终结符	FIRST	FOLLOW
E	{ (, int }	{ ), $ }
E’	{ +, ε}	{ ), $ }
T	{ (, int }	{ +, ), $}
T’	{ *, ε }	{ +, ), $}
F	{ (, int }	{ *, +, ), $ }

注意上面求 T和 T’ 的FOLLOW集合，步骤如下：

$\text{FOLLOW}(T) = (\text{FIRST}(E')-\{\epsilon\})\cup \text{FOLLOW}(E')$

这是由于 FIRST(E’)包含有 ε，因此，可以将左部 FOLLOW(E)或 FOLLOW(E’) 加入到 FOLLOW(T)，得到 FOLLOW(T) = { ), $ }，同时 符号 + 又是 ( FIRST(E’) -{ε} ) 的且在 T下一个字符，因此最终 FOLLOW(T) = {+,),$} = FOLLOW(T’)

同理对于 F 的FOLLOW集合，求法如下：

$\text{FOLLOW(F)}=(\text{FIRST}(T')-\{\epsilon\})\cup \text{FOLLOW}(T)\\ = \{*\}\cup\{+,),\$\}\\ = \{*,+,),\$\}$

首先看第一个产生式： E -> T E’ 。 First(T E’) = { (, int } 。FIRST中所有终结符号为 ( ，int

因此 M[E, (] => "E -> T E'" , M[E, int] => "E -> T E'"。写成表格的形式：

	int	+	*	(	)	$
E	E -> T E’			E -> T E’
E’
T
T’
F

接下来看第二个产生式： E’ –> + T E’ 。 First( + T E’ ) = { + } 。因此 M[E', +] = "E' -> + T E'"。

再看第三个产生式： E’ -> ε 。First( ε ) = { ε } ，且 Follow(E’) = { $ ) }，该FOLLOW所有终结符号为 )，$ ，因此 M[E’, $] = M[E’, )] = "E' -> ε" 。都写到表格里面：

	int	+	*	(	)	$
E	E -> T E’			E -> T E’
E’		E’ –> + T E’			E’ -> ε	E’ -> ε
T
T’
F

重复以上方法，最终的分析表为：

	int	+	*	(	)	$
E	E -> T E’			E -> T E’
E’		E’ –> + T E’			E’ -> ε	E’ -> ε
T	T –> F T’			T –> F T’
T’		T’ –> ε	T’ –> * F T’		T’ –> ε	T’ –> ε
F	F –> int			F –> ( E )

解析句子 int + int * int ：

Parse Stack	Remaining Input	Parse Action
E $	int + int * int $	Predict E -> T E’
T E’ $	int + int * int $	Predict T -> F T’
F T’ E’ $	int + int * int $	Predict F -> int
int T’ E’ $	int + int * int $	Match int
T’ E’ $	+ int * int $	Match int
T’ E’ $	+ int * int $	Predict T’ –> ε
E’ $	+ int * int $	Predict E’ –> + T E’
+ T E’ $	+ int * int $	Match +
T E’ $	int * int $	Predict T –> F T’
F T’ E’ $	int * int $	Predict F –> int
int T’ E’ $	int * int $	Match int
T’ E’ $	* int $	Predict T’ –> * F T’
* F T’ E’ $	* int $	Match *
F T’ E’ $	int $	Predict F –> int
int T’ E’ $	int $	Match int
T’ E’ $	$	Predict T’ –> ε
E’ $	$	Predict E’ –> ε
$	$	Match $, ACCEPT

LL(1) 分析法的优点是不需要回溯，构造方法较简单，且分析速度非常快，每读到第一个符号就可以预测出整个产生式来。缺点是对语法的限制太强，它要求同一个非终结符的不同产生式的首字符集合互不相交，能满足此要求的语法相当少，而将一个不满足此要求的语法改写到满足要求也相当不容易。因此， LL(1) 分析法目前已经应用的比较少了。左递归和二义性不可能是LL(1)

参考文章： https://pandolia.net/tinyc/ch10_top_down_parse.html

错误例子

下面举一个错误的例子来说明不是所有的文法都可以用LL(1)表示，下面这个文法抽象表示一个悬空-else的问题。

S  -> iEtSS'|a
S' -> eS|ε
E  -> b

计算得到FIRST和FOLLOW集合

非终结符号	FIRST	FOLLOW
S	{ i, a }	{ eS, $ }
S’	{ e, ε }	{ eS, $ }
E	{ b }	{ t, $}

对于上面的产生式 S’ ，它的FOLLOW(S’)={ eS, $} 是因为在第一个产生式中 S’ 在末尾，且 S’ 含有一个空字符epsilon，所以 FOLLOW(S) 应该加入到 FOLLOW(S’) 中，也就是 SS’ 后面的 S’，替换了就是 eS，该过程为 SS’ -> SeS。

对于FIRST和FOLLOW的个人感悟

总之，现在对于FIRST和FOLLOW有了更深入的了解。也就是：FIRST 一般用在右边的产生式体，来得到下一个与之匹配的输入符号（匹配正确和失败两种状态），然后用该产生式体替换到左部抽象的非终结符号；而FOLLOW则是对于某一个形如含有 S->ε 之类含有 epsilon 的产生式，当前 非终结符号S 可以 跳过 ，直接匹配下一个待替换符号，然后用该符号来替换空字符 epsilon，而这个 “下一个待替换符号” 一般是根据FOLLOW中的终结符号来确定下一步应该处理哪一个符号。

即 A [S->ε] xyz … => A FOLLOW(S) … 其中 xyz可能位于 FOLLOW(S) 中，表明 S 的下一个待替换符号应该在 FOLLOW中寻找，以便能够替换到空字符 epsilon。

相反，如果一个产生式没有含有 epsilon 空字符，那么也就是说该产生式可以直接根据 FIRST来进行替换，不需要通过epsilon引用FOLLOW中的符号来替换下一个符号。

FOLLOW的本意应该是 预测下一步要确定匹配/替换的符号的集合，因为下一步中可能有多个预测要确定的符号，所以LL(1)需要构造一个预测分析表来确定下一步应该怎么做。

得到的M表为

	a	b	e	i	t	$
S	S->a			S->iEtSS’
S’			S’->ε 和 S’->eS			S’->ε
E		E->b

注意 M[S',e] 包含了两个条目，因此该文法是二义性的。

表驱动的预测语法分析

• 输入：一个串w,文法 G，预测分析表 M
• 输出：如果串w在 L(G)中，输出w的一个最左推导；否则输出一个错误提示。