之前已经简单地介绍了LZW 编码实现的原理，它由一个初始字典在编码/解码的过程中不断的扩增字典内容，从而在下一次编码/解码遇到重复的文本串时从字典中找出之前的代码并写入文本文件，这样就避免了重复的文本而达到文本文件空间缩小的目的。本文主要从简单介绍哈夫曼树过渡到编码解码内容。

哈夫曼树

哈夫曼树也可以称作霍夫曼树（Huffman Tree），实际上它是一颗最优二叉树。它的最优主要体现在它的加权路径长度WPL(weighted path length) 最小！为什么最小，下文有解释…
注意，节点的加权路径长度是指从根节点到该节点之间的路径长度与该节点权值的乘积。而WPL指的是所有叶子节点的加权路径长度总和。

哈夫曼树详细信息可以参考这位大佬的文章 数据结构和算法——Huffman树和Huffman编码 。毕竟本文主要是介绍哈夫曼的编码解码过程，而且理解哈夫曼树也花不了多长时间…

编码

哈夫曼编码与LZW编码均为无损数据压缩算法的实现，哈夫曼编码最明显的一个特点是无需存储8位的字符，只需要存储01比特流即可，它是用较少的比特来表示出现频率高的字符，用较多的比特表示出现频率低的字符，即可变长编码（从哈夫曼树的角度理解就是字符出现频率/权值高的位于树的顶层，反之位于树的底层）。这样的话能够比较容易节省空间（毕竟写入以位为单位的数据总比写入以字节为单位的要节省空间）。

无论是编码还是解码，都需要构造哈夫曼树，并且得到一个哈夫曼编码表，之后我们就是利用这个表将ASCII文件中出现的字符所对应的二进制bit流写入到压缩文件中。

假设压缩文件为ASCII文件，那么在构造哈夫曼树之前还需要统计ASCII文件中每个ASCII字符出现的频率，也就是哈夫曼树每个节点的权值。统计方法很简单，直接扫描一遍文件即可。

那么如何构造哈夫曼树呢？从字符出现频率/权值高的位于树的顶层，反之位于树的底层可知，我们需要利用之前已经统计好的字符频率表F(c)来构造哈夫曼树，常见的方法是通过优先级队列来完成构造，除此之外还可以通过排序的方法完成。总之，构造的贪婪准则是每次选取两个出现频率最小(a,b)的节点作为子节点，其父节点表示子节点出现的总频率(a+b)，直到剩余根节点为止，这里的节点指的是F©中每个出现频率大于0的字符。宏观上来看，构造哈夫曼树是自底向上进行的。

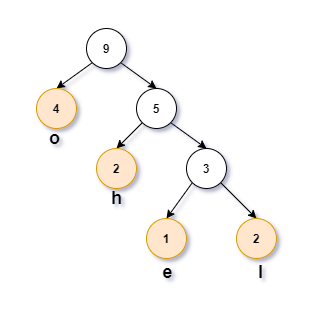
举个例子，假设有一段文本S=hhelloooo，首先统计每个字符出现频率：

character	h	e	l	o
frequency	2	1	2	4

接着利用这个表构造哈夫曼树如下图所示

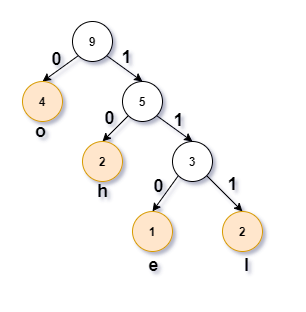
假设将父节点与左节点相连接分支标记为0、右节点的标记为1（也可以这样理解：0表示向左子树移动一步、1表示向右子树移动一步）

那么字符h在哈夫曼树中表示二进制串为 10，同样e、l、o对应的二进制串分别为110、111、0。
于是进一步得到了一个完整的表格，从这个表格可以得到的信息有：

• 字符到二进制代码的映射表
• 字符的频率表

character	h	e	l	o
frequency	2	1	2	4
bit stream	10	110	111	0

将字符串 hhelloooo 每个出现的字符用二进制表示就是： 10.10.110.111.111.0.0.0.0。

注意，我们还发现字符h、e、l、o始终位于叶子节点，这样有什么意义吗？回答这个问题之前先引入一个概念：变长前缀码，大意是：没有一个代码是另一个代码的前缀 。 这句话我是摘自《数据结构算法与应用》，而《算法》第四版中是这样描述的：如果所有字符编码都不会成为其他字符编码的前缀，那么就不需要分隔符了 。其实这很容易理解，如果存在一个二进制代码是另外某一个二进制代码的前缀，那么在解码的过程中就会无法判断出该二进制代码属于哪个原始字符。因此，要避免这种情况，最好的办法就是将字符节点置于叶子节点，这样在解码的过程中自顶向下的寻找原始字符就可以完成了。

现在再来讨论另一个问题，毕竟哈夫曼编码是解压缩算法嘛，那么其压缩效率如何呢？

比如上面的字符串hhelloooo，由于每个ASCII码占一个字节，总共9bytes=72bits，编码后的二进制串 10101101,11111000,0 总共17bits，故压缩率大约是 23.6%，还行。
再来看一个全是字母a且长度为约62k字节的字符串，压缩后的文件大小仅为5字节！现在仅仅改变一个字母a为b，原文件大小不变，此时压缩后的文件大小约为7.7K字节！

咳咳，现在回答之前的那个问题：为什么加权路径长度WPL是最小的。我们不妨来算一下现在这颗哈夫曼树的WPL是多少呢，
其WPL为：1x4+2x2+3x1+3x2=4+4+3+6=17。这与压缩后的文件大小相等，这也说明了WPL越小，压缩文件体积越小，但也不可能为0。
这时候得到一个结论：对于任意变长前缀码，编码后的二进制bit流的长度等于相应的哈夫曼树的WPL。

注意：在某些情况下压缩率甚至会超过100%！

可见哈夫曼编码对于文件压缩也是有要求的。

1.必须尽量利用被压缩的数据流中的已知结构；
2.小规模的字母表；
3.较长的连续相同的位或字符；
4.频繁使用的字符；
5.较长的连续重复的位或字符。

那么问题来了，既然能够压缩文件，那么也得必须完全成功解压文件才行啊，不然文件是真的损坏了哭都来不及:)。总所周知LZW 编码在实现编码的整个过程中没有将整个字典写入压缩文件，甚至在解码时也是没有一个完整的字典，这是LZW的独特之处。而哈夫曼编码则不同，它是需要写入相关信息的！这样在解码时才能够重构哈夫曼树。这个相关信息可以是字符到二进制代码的映射表bitstream©或者每个字符的频率表f©。不过《算法》第四版里面并没有用的以上两种方法，而是写入一个哈夫曼树结构（将哈夫曼树编码为bit流），这样做的直接目的是防止不必要的空间浪费。
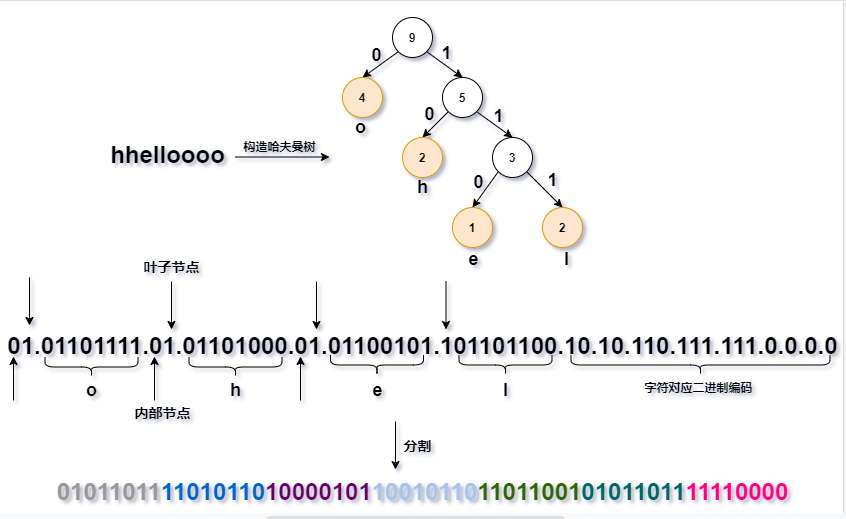
至于怎么编码，其实就是通过一次前序遍历将内部节点和叶子节点的开关bit写入压缩文件中。比如下面这张图

在一次前序遍历过程中，如果遇到内部节点就写入0bit，如果是叶子节点除了写入1bit外还需要将字符的ASCII码（8bits）也写入文件，最后再写入变长前缀码。这样做的理由方便解码时重构哈夫曼树。
总之需要写入文件的内容有：编码哈夫曼树的bits流+字符个数(32bits)+对应字符的二进制代码（或者称为变长前缀码）。上面的图没有标字符个数的二进制（毕竟这个例子才只有9个字符，不可能画那么多0吧）。

当然了，不是每次都恰好将每8bits一个字节写入文件，可能最后就会多出N位$( 1 \le N \le 7)$。要知道目前标准C++只能操作字节流，还不能操作位流（Java有BinaryStdIn/Out）。解决方法很简单粗暴，不足8位的就在后面补0。

现在小结一下，要实现哈夫曼压缩算法，需要以下几个步骤：

• 从文件输入流统计在ASCII码范围内字符出现频率；
• 利用频率表构造哈夫曼树；
• 利用哈夫曼树构造哈夫曼编码表（如a:10010）；
• 写入哈夫曼树/bitstream©/f©；
• 写入字符个数，毕竟解码可不知道有多少个字符；
• 从哈夫曼编码表写入所有字符对应的二进制编码；
• 压缩结束。

解码

解码就是编码的逆操作，不过一些细节还是需要注意的。
还是以上面那个例子来说吧(⊙﹏⊙)
01(01101111)01(01101000)01(01100101)1(01101100)+10101101111110000

解码的第一步肯定是读取前面那一坨已经将哈夫曼树编码成bit流的二进制串，关键是读取了该怎么构造出哈夫曼树。记得之前编码时我们是走一次前序遍历才将哈夫曼树编码成bit流，那么解码又有何不可呢？如果读取的一个bit是1，这说明该处是叶子节点(new)，那么接着再读取1byte就能够得到一个ASCII码，然后结束；如果读取到0bit，说明是这是一个内部节点(new)，将该内部节点作为父节点后那么继续递归，直到遍历完所有叶子节点。

至此，我们已经通过bit流构造出了哈夫曼树，接着再读取32bits或者64bits，总之是一个记录着字符个数的整数。

最后一步就是解析变长前缀码 10.10.110.111.111.0.0.0.0 。观察这一串二进制文本，它被分割的份数也就是他对应的字符总数，这也是为什么需要写入字符个数的原因，此时我们并不知道压缩文件总共有多少bits，但是我们知道它有N个字符，那么就可以通过哈夫曼树反解出所有的原始字符并写入解压文件。当然了，如果已经知道压缩文件有多少个bits，那么就没必要这个N了，直接的方法就是一位一位的读取并根据哈夫曼树解析出原始字符，不过就是另外一种方法，这里就不讨论了。

小结一下，解码过程可以分为以下几个步骤：

• 读取压缩文件bit流重构哈夫曼树；
• 读取字符个数N；
• 根据哈夫曼树、N解析出原始字符，方法是自顶向下轮循解析；
• 解压结束。

解析位流

代码参考了《算法》第四版的，不过书上是Java版本的，而且最dan teng的就是解析位流，无论是C的fread、fwrite、还是C++的basic_ifstream、basic_ofstream，都至少一个字节，根本不能直接操作位流，而Java的BinaryStdIn/Out可以操作位流。无奈之下，只能自己写一个简单地可以控制位流的类，原理也很简单，就是一些&|<<>>…（后来发现网上已经有大佬完成了…）然后再改写Java版本的哈夫曼编码实现，
本来想着能简就简的…
想着能简就简的…
能简就简的…
简简的…
简的…
简.
.

代码就不放了…
码不放了…
码了…
了…
…
.

参考

《算法》第四版
《数据结构算法与应用》
Huffman coding
哈夫曼树