数据结构-队列

队列是一种先进先出(FIFO)的数据结构，与栈(后进先出LIFO)不同，但两者都是线性结构，因此可以用线性表去描述队列，本文主要是用数组去实现一个简单的队列

队列

对一个队列操作，只能从队首删除元素，队尾插入元素，因此我们可以定义两个队列元素指针front,back，用于跟踪队列首尾元素。
C++ STL实现了队列数据结构，我们用时不可能立即手写一个队列，因而只需include头文件即可，不过对于队列这一数据结构原理还是要理解的

我们知道，队列可以用数组或链表实现，不过本文是以数组来讲述的因此较为简单

插入

队列插入一个元素时，先将队尾指针back+1，使其指向下一个空闲区
域，然后在插入元素。复杂度为O(1)

删除

删除队首元素有两种策略

  1. 直接整个数组左移一位，front不变，back向前移动一位。复杂度O(n)
  2. 数组不移动，front移动到下一位，back不变。复杂度O(1)

显然删除操作情况1不能接受，然而对于删除操作情况2，会导致数组空间浪费，这是因为front指针之前的区域未能被利用，而back指针之后的区域显然不够(这里在没有考虑数组变增的情况下)。

如果将数组“串”起来怎样？事实上确实可以，这种数组叫环形数组，用此类型数组实现的队列称为循环队列 且其插入删除复杂度均为O(1)

环形数组表示队列通过下面公式实现:

location(i)=(location(front)+i)%arrayLength

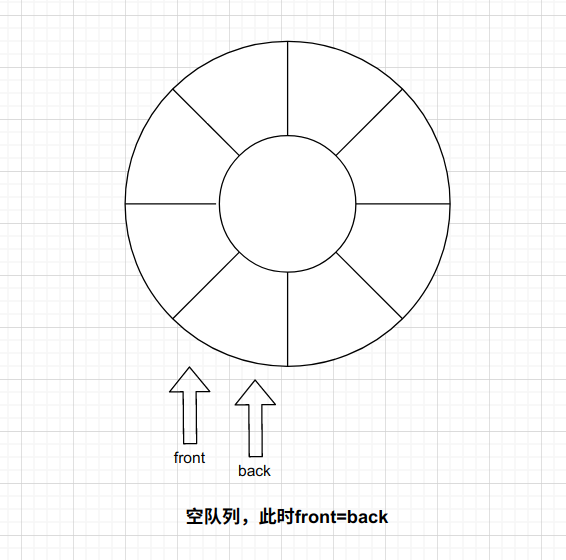
如下图一个空队列，此时 front=back

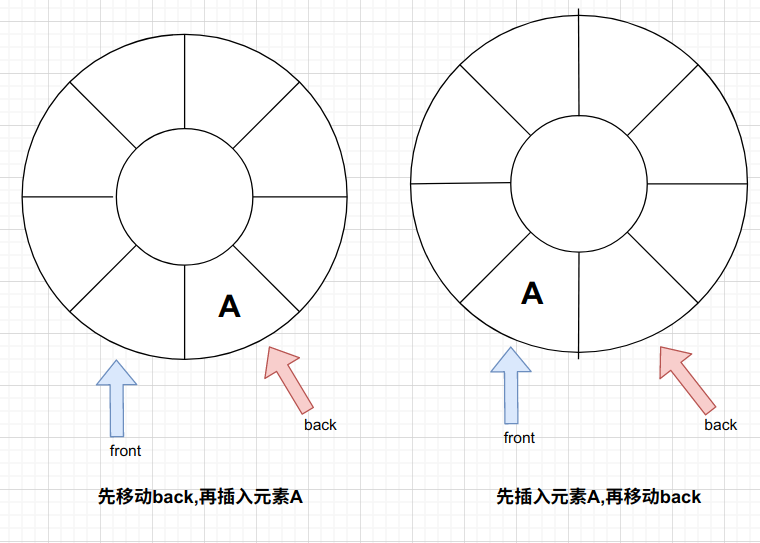
当插入一个元素时，也有两种策略

1.先移动back，后插入元素。那么front指向元素为"空"
2.先插入元素，后移动back。那么back指向元素为"空"

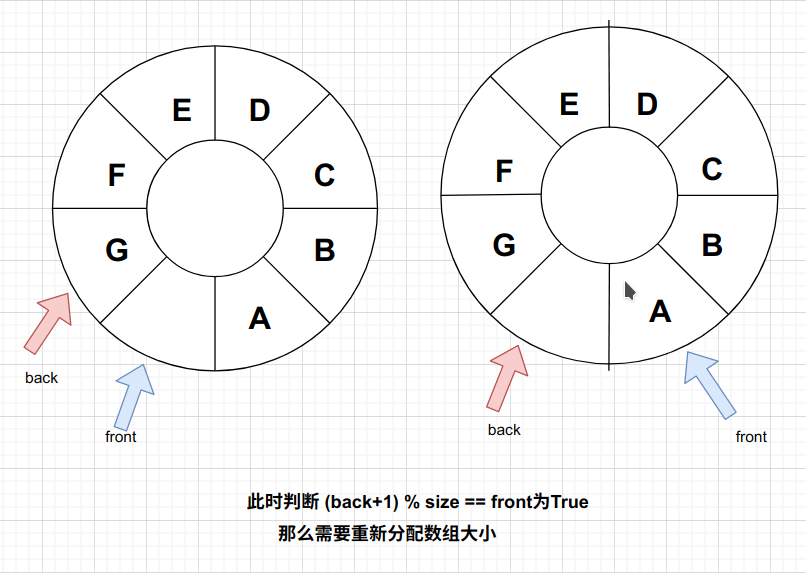
每次插入都需要判断 (back+1)%size == front ，为什么？我们知道，初始时front=back表示空队列，那么当插入元素数量达到数组长度此时front=back！这表示这个队列满的还是空的？因此我们预留一个位置，也就是队列不能插满。即

front=back 空队列
(back+1)%size = front 满队列

如何获取队列中第n个元素在数组中的下标？
假设front=10，back=4。

因此我们用C++实现该循环队列

队列实现

队列抽象数据类型

1
2
3
4
5
6
7
8
9
10
11
template<class T>
class QueueBase{
public:
    virtual ~QueueBase(){}
    virtual void push_back(const T &)=0;
    virtual void pop_front()=0;
    virtual T & front()=0;
    virtual T & back()=0;
    virtual bool empty()=0;
    virtual int size()=0;
};

之后在另外定义一个派生类继承QueueBase接口。
我是按照策略2来插入元素的，代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
template<class T>
class arrayQueue{
private:
    T *m_array;
    int m_capacity;
    int front;
    int back;
public:
    arrayQueue(int initCapacity=10){
        m_capacity=initCapacity;
        m_array=new T[m_capacity];
        front=0;
        back=0;
    }
    ~arrayQueue(){delete []m_array;}
    void push_back(const T &);
    void pop_front();
    T & Front(){
        return m_array[front];
    }
    T & Back(){
        return m_array[back-1];
    }
    bool empty(){return front==back;}
    int size(){
        if(front<back)
            return back-front;
        else 
            return back+m_capacity-front;
    }
    void changeLength(T* &,int,int);
    void output(){
        if(empty())return;
        // 情况1
        if(front<back){
            for (int i = front; i < back; i++){
                cout<<"["<<i<<"] "<<m_array[i]<<"\n";
            }
        // 情况2
        }else{
            for (int i = front; i < m_capacity; i++){
                cout<<"["<<i<<"] "<<m_array[i]<<"\n";
            }
            for (int i = 0; i < back; i++){
                cout<<"["<<i<<"] "<<m_array[i]<<"\n";
            }
        }
    }
};

template<class T>
void arrayQueue<T>::push_back(const T &element){
    // 满队列
    if((back+1)%m_capacity==front){
        // 数组倍增
        changeLength(m_array,m_capacity,m_capacity*2);
        m_capacity*=2;
    }
    // 按照策略2插入: 先插入元素，后移动back
    m_array[back]=element;
    // 注意，此处不能直接 back++，这样做会使back超出数组长度从而导致数组访问越界
    // 相反，(back+1)%m_capacity 会使back指针回到数组起始处继续插入
    back=(back+1)%m_capacity;
}
template<class T>
void arrayQueue<T>::pop_front(){
    // 判空
    if(back==front)return;
    m_array[front].~T();
    // 同样这里也是控制front只能处于数组之间
    front=(front+1)%this->m_capacity;
}
template<class T>
void arrayQueue<T>::changeLength(T* &array,int oldLength,int newLength){
    if(newLength<0)return;
    T* temp=new T[newLength];
    // 从有效元素开始复制
    if(front<back)
        // 没有形成环
        std::copy(array+front,array+back,temp);
    else{
        // 形成环
        std::copy(array+front,array+oldLength,temp);
        std::copy(array,array+back,temp+oldLength-front);
        // 重新设置front,back
        front=0;
        back=oldLength-1;
    }
    delete []array;
    array=temp;
}

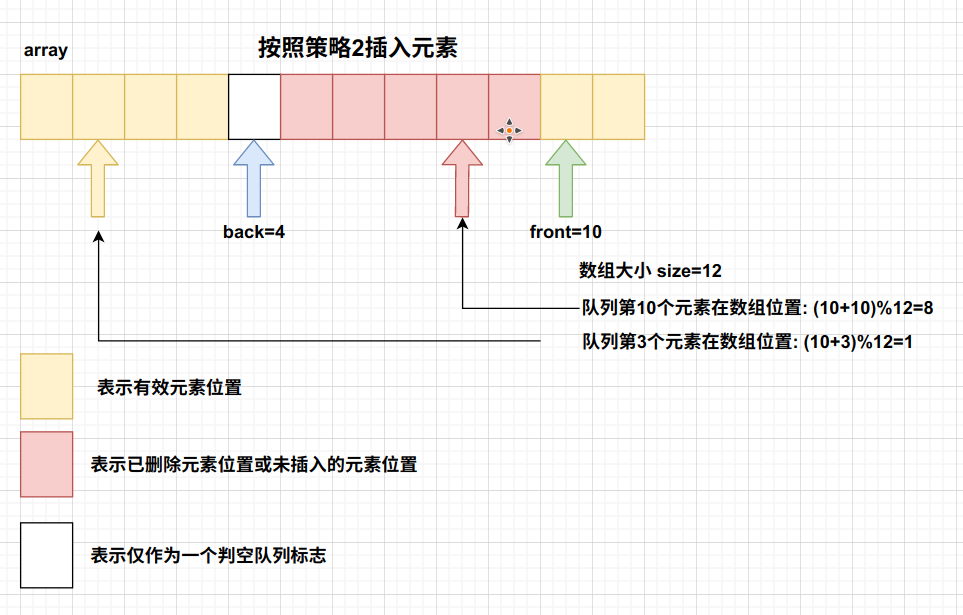
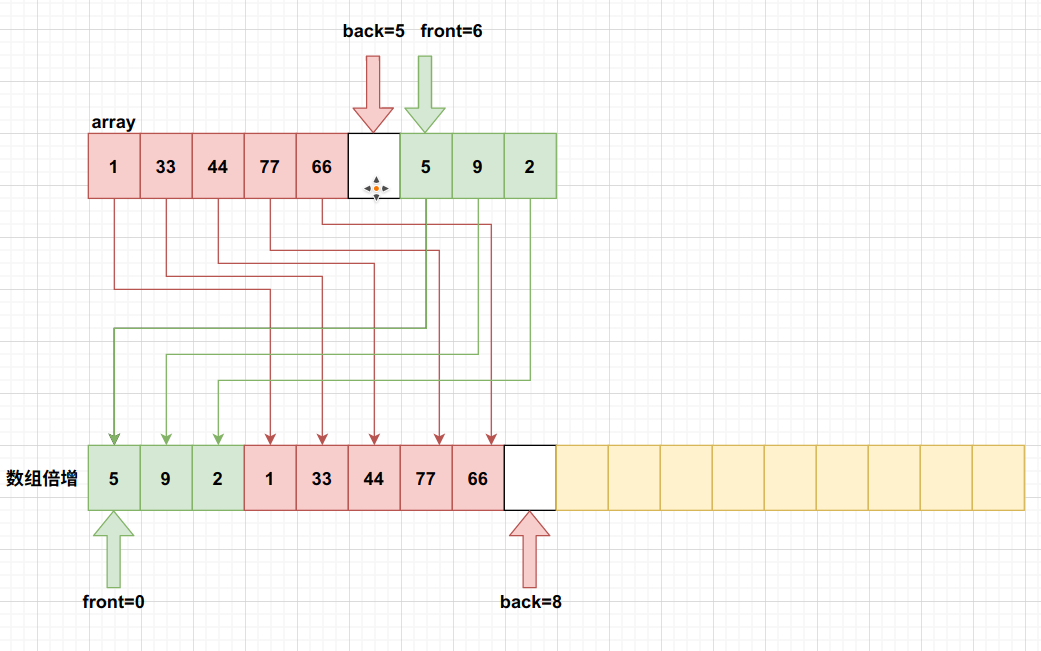
我认为比较难理解的是changeLength改变数组长度函数，其实用一张图表示就很简单了

测试

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<iostream>
using namespace std;
int main(){
    arrayQueue<int>q(5);
    q.push_back(1);
    q.push_back(2);
    q.push_back(3);
    q.push_back(4);
    q.push_back(40);
    q.push_back(400);
    q.push_back(4000);
    q.push_back(40000);

    q.pop_front();
    q.pop_front();
    q.pop_front();
    q.pop_front();
    q.pop_front();
    q.pop_front();

    q.push_back(5);
    q.push_back(6);
    q.push_back(7);
    q.push_back(8);
    q.push_back(9);

    q.output();
    cout<<"size: "<<q.size()<<endl;
    cout<<"front: "<<q.Front()<<endl;
    cout<<"back: "<<q.Back()<<endl;
    return 0;
}

输出

1
2
3
4
5
6
7
8
9
10
[6] 4000
[7] 40000
[8] 5
[9] 6
[0] 7
[1] 8
[2] 9
size: 7
front: 4000
back: 9

STL queue

将自己写的arrayQueue和STL queue分别测试，看看谁快些，这里我仅仅测试了先插入完成后再删除。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
int main(){
    arrayQueue<int>q2;
    int n=100000000;
    CClock::start_timeclock();
    for (int i = 0; i < n; i++){
        q2.push_back(i);
    }
    for (int i = 0; i < n; i++){
        q2.pop_front();
    }
    q2.output();
    CClock::stop_timeclock();
    auto t1=CClock::time_duration();

    CClock::start_timeclock();
    queue<int>q3;
    for (int i = 0; i < n; i++){
        q3.push(i);
    }
    for (int i = 0; i < n; i++){
        q3.pop();
    }
    CClock::stop_timeclock();
    auto t2=CClock::time_duration();

    cout<<"arrayQueue: "<<t1<<endl;
    cout<<"queue: "<<t2<<endl;
}

输出结果，单位秒

1
2
arrayQueue: 2.32446
queue: 2.63278

不知道该如何表达…
(⊙o⊙)…

结尾

bye~